www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Integral Lipat Tiga › Integral Lipat Tiga dalam Koordinat Kartesius - Materi, Contoh Soal dan Pembahasan
Integral Lipat
Integral Lipat Tiga dalam Koordinat Kartesius - Materi, Contoh Soal dan Pembahasan
Integral lipat tiga adalah integral untuk fungsi tiga peubah. Di artikel ini kita secara khusus membahas integral lipat tiga dalam koordinat kartesius.
Konsep yang diwujudkan dalam integral tunggal dan lipat dua dapat meluas secara wajar ke integral lipat tiga, dan bahkan ke lipat \(n\). Integral lipat tiga adalah integral untuk fungsi tiga peubah. Di sini kita secara khusus akan membahas integral lipat tiga dalam koordinat kartesius.
Seperti pada integral tunggal dan lipat dua, penjelasan mengenai integral lipat tiga akan dimulai dengan penjumlahan Riemann. Perhatikan suatu fungsi \(f\) tiga peubah yang didefinisikan atas suatu daerah berbentuk balok B dengan sisi-sisi sejajar sumbu-sumbu koordinat. Kita tidak dapat lagi menggambarkan grafik \(f\) (dimensi empat yang diinginkan), tetapi kita dapat menggambar \(B\) (Gambar 1).

Gambar 1
Bentuklah suatu partisi \(P\) dari \(B\) dengan melewatkan bidang-bidang melalui \(B\) sejajar bidang koordinat, jadi memotong \(B\) ke dalam balok-balok bagian \(B_1,B_2,…,B_n\); satu yang khusus \(B_k\) – diperlihatkan pada Gambar 1. Pada \(B_k\), ambil satu titik contoh \((\overline{x}_k, \ \overline{x}_k, \ \overline{x}_k)\) dan perhatikan penjumlahan Riemann

dengan \(ΔV_k=Δx_k \ Δy_k \ Δz_k\) adalah volume \(B_k\). Andaikan norma partisi \(|P|\) ini adalah panjang diagonal terpanjang dari semua balok bagian. Maka kita definisikan integral lipat tiga dengan

asalkan limit ini ada.
Pertanyaan tentang fungsi apa yang dapat diintegralkan muncul di sini, sama halnya seperti pada integral tunggal dan lipat dua. Tentu saja cukup bahwa \(f\) kontinu di \(B\).
Contoh 1:
Hitung \(∭_V x^2 yz \ dV\), dengan \(B\) adalah kotak

Penyelesaian:

Terdapat enam urutan pengintegralan yang mungkin. Yang mana saja di antara mereka akan menghasilkan jawaban 7/3.
Daerah Umum
Perhatikan suatu daerah \(S\) terbatas dan tertutup di ruang dimensi-tiga dan dilingkungi di dalam suatu balok \(B\), seperti diperlihatkan pada Gambar 2. Andaikan \(f(x,y,z)\) didefinisikan pada \(S\) dan berikan \(f\) nilai nol di luar \(S\). Kemudian kita definisikan

Integral di ruas kanan telah kita definisikan di atas, tetapi tidak berarti bahwa integral tersebut mudah untuk dihitung. Sebenarnya, jika himpunan \(S\) cukup rumit, kita mungkin tidak mampu melakukan perhitungan itu.
Andaikan \(S\) adalah himpunan \(z\) sederhana (garis-garis tegak memotong \(S\) menurut ruas garis tunggal) dan andaikan \(S_{xy}\) adalah proyeksinya pada bidang \(xy\) (Gambar 3). Maka

Sebagai tambahan, jika \(S_{xy}\) adalah himpunan \(y\) sederhana (seperti diperlihatkan pada Gambar 3), kita dapat mengulang-tulis integral lipat dua sebelah luar sebagai integral lipat.

Gambar 2 (Kiri) dan 3 (Kanan)
Urutan pengintegralan lain boleh jadi memungkinkan, tergantung pada bentuk \(S\), tetapi dalam tiap kasus kita seharusnya mengharapkan limit dari integral sebelah dalam berupa fungsi dua peubah, yang berada pada integral tengah berupa fungsi satu peubah, dan yang di sebelah luar berupa konstanta.
Contoh 2:
Hitung integral lipat

Penyelesaian

Contoh 3:
Hitung integral lipat tiga untuk \(f(x,y,z)=2xyz\) dalam daerah pejal \(S\) yang dibatasi oleh tabung parabol \(z=2-\frac{1}{2} x^2\) dan bidang-bidang \(z = 0, \ y = x\), dan \(y = 0\).

Gambar 4
Penyelesaian
Daerah pejal \(S\) diperlihatkan pada Gambar 4. Integral lipat tiga

dapat dihitung dengan integral lipat.
Pertama perhatikan bahwa \(S\) adalah suatu himpunan \(z\) sederhana dan bahwa proyeksinya \(S_{xy}\) pada bidang \(xy\) adalah \(y\) sederhana (juga \(x\) sederhana). Jadi,
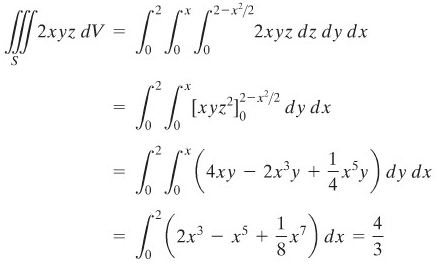
Terdapat beberapa urutan pengintegralan berbeda yang memungkinkan dalam Contoh 3. Kita ilustrasikan cara lain untuk mengerjakan soal pada Contoh 3.
Contoh 4:
Hitung integral dari Contoh 3 dengan mengerjakan pengintegralan dalam urutan \(dy \ dx \ dz\).
Penyelesaian
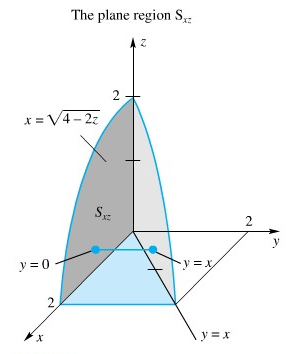
Gambar 5.
Perhatikan bahwa benda pejal \(S\) adalah \(y\) sederhana dan ia diproyeksikan ke dalam himpunan bidang \(S_{xz}\) yang diperlihatkan pada Gambar 5. Pertama kita integralkan sepanjang garis horizontal dari \(y = 0\) ke \(y = x\); kemudian kita integralkan hasilnya terhadap \(S_{xz}\).

Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
You can’t fall if you don’t climb. But there’s no joy in living your whole life on the ground.
Unknown
