Kalkulus II   »   Transformasi Koordinat   ›  Jacobian - Materi, Contoh Soal dan Pembahasan

Jacobian

Jacobian - Materi, Contoh Soal dan Pembahasan

Matriks Jacobian atau biasa disebut Jacobian didefinisikan sebagai matriks yang mengandung turunan parsial orde pertama untuk suatu fungsi.

---

Matriks Jacobian atau biasa disebut Jacobian didefinisikan sebagai matriks yang mengandung turunan parsial orde pertama untuk suatu fungsi. Matriks Jacobian bisa berupa matriks persegi panjang (rectangular matrix) di mana jumlah baris dan kolom tidak sama atau bisa berupa matriks kuadrat yang mana jumlah baris dan kolom adalah sama.

Misalkan terdapat himpunan n persamaan y = f(x) dalam n variabel \(x_1,\cdots,x_n\), yang dituliskan sebagai:

atau secara lebih eksplisit sebagai

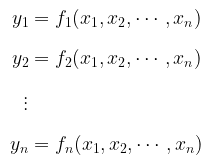
maka, matriks Jacobian definisikan sebagai:

Perhatikan bahwa huruf J menyatakan Jacobian. Selain dengan huruf J, Jacobian juga dapat dinyatakan dengan lambang \( \frac{\partial (y_1,\cdots,y_n)}{\partial (x_1,\cdots,x_n)} \).

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.