Contoh 2:

Apakah \(\displaystyle{\sum_{n=1}^{\infty} \frac{n}{2^n (n+1)}} \) konvergen atau divergen?

Penyelesaian:

Agaknya deret ini konvergen, sebab untuk \(n\) cukup besar suku ke-\(n\) mirip dengan \((1/2)^n\). Tepatnya

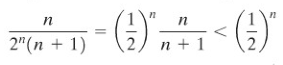
Deret geometri \(∑(1/2)^n\) adalah konvergen, sebab rasionya adalah \(½\). Jadi deret yang diketahui juga konvergen.

Contoh 3:

Apakah \(\displaystyle{\sum_{k=1}^{\infty} \frac{1}{\sqrt{k-1/2}}} \) konvergen atau divergen?

Penyelesaian:

Bandingkan kedua deret:

Karena \(\frac{a_k}{b_k} > 1\), maka \(a_k > b_k\) atau \(b_k < a_k\) dan karena \(a_k\) konvergen, maka \(b_k\) juga konvergen.

Contoh 4:

Apakah \(\displaystyle{\sum_{n=1}^{\infty} \frac{1}{\sqrt{n} + 1/2}} \) konvergen atau divergen?

Penyelesaian:

Bandingkan kedua deret:

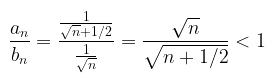
Karena \(\frac{a_n}{b_n} < 1\), maka \(a_n < b_n\) dan karena deret yang lebih besar \(b_n\) divergen (berdasarkan uji deret-p), maka tidak bisa dipakai uji banding.

Contoh 5:

Apakah \(\displaystyle{\sum_{k=1}^{\infty} \frac{k}{k^2+1}} \) konvergen atau divergen?

Penyelesaian:

Misalkan, \( a_k = \frac{k}{k^2+1} \) dan \( b_k = \frac{1}{k} \).

Dengan membandingkan kedua deret tersebut, diperoleh

Karena \(\frac{a_k}{b_k} < 1 \), maka \(a_k < b_k\).

Karena deret yang lebih besar (\(b_k\)) divergen, maka belum tentu deret yang lebih kecil divergen sehingga untuk menentukan apakah deret \(\displaystyle{\sum_{k=1}^{\infty} \frac{k}{k^2+1}} \) konvergen atau divergen harus ganti uji yang lain.