www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Turunan Fungsi Peubah Banyak › Aturan Rantai untuk Mencari Turunan Fungsi Peubah Banyak - Materi, Contoh Soal dan Pembahasan
Turunan
Aturan Rantai untuk Mencari Turunan Fungsi Peubah Banyak - Materi, Contoh Soal dan Pembahasan
Aturan rantai untuk fungsi-fungsi komposisi satu peubah telah dipelajari pada kalkulus I. Pada artikel ini, kita akan membahas perluasan dari aturan rantai ini khususnya untuk fungsi-fungsi beberapa peubah.
Aturan rantai untuk fungsi-fungsi komposisi satu peubah telah kita pelajari pada materi kalkulus I. Sebagai contoh, jika \(y=f(x(t))\), dengan \(f\) dan \(x\) keduanya fungsi yang dapat didiferensialkan, maka turunan \(y\) terhadap \(t\) dapat dinyatakan dengan
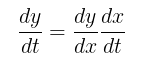
Pada artikel ini, kita akan membahas perluasan dari aturan rantai ini khususnya untuk fungsi-fungsi beberapa peubah. Terdapat dua versi dari aturan rantai untuk beberapa peubah.
Versi pertama
Jika \(z=f(x,y)\), dengan \(x\) dan \(y\) adalah fungsi \(t\), maka masuk akal menanyakan \(dz/dt\), dan seharusnya ada sebuah rumus untuknya. Kita nyatakan dalam teorema berikut.
Teorema A: Aturan Rantai
Andaikan \(x=x(t)\) dan \(y=y(t)\) dapat didiferensialkan di \(t\) dan andaikan \(z=f(x,y)\) dapat didiferensialkan di \((x(t),y(t))\). Maka \(z=f(x(t), y(t))\) dapat didiferensialkan di \(t\), yakni
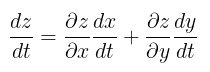
Contoh 1:
Misalkan \(z=x^3 y\) dengan \(x=2t\) dan \(y=t^2\). Tentukan \(dz/dt\).
Penyelesaian:

Tentu saja kita dapat menyelesaikan Contoh 1 di atas tanpa menerapkan Aturan Rantai. Dengan substitusi langsung, kita peroleh

Contoh 2:
Misalkan bahwa sebuah tabung lingkaran tegak pejal dipanasi, radiusnya bertambah pada laju 0,2 sentimeter per jam dan tingginya bertambah pada laju 0,5 sentimeter per jam. Tentukan laju pertambahan luas permukaan terhadap waktu pada saat radius sama dengan 10 sentimeter dan tinggi sama dengan 100 sentimeter.
Penyelesaian:
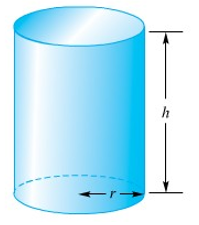
Gambar 1.
Rumus total luas permukaan sebuah tabung (Gambar 1) adalah
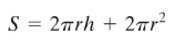
Jadi,

Pada \(r = 10\) dan \(h = 100\), maka

Hasil dalam Teorema A dapat diperluas ke sebuah fungsi tiga peubah. Perhatikan contoh berikut ini.
Contoh 3:
Andaikan \(w=x^2 y+y+xz\), dengan \(x=\cos{θ},y=\sin{θ}\),dan \(z=θ^2\). Tentukan \(dw/dθ\) dan hitung nilainya di \(θ=π/3\).
Penyelesaian:

Pada \(θ=π/3\), maka
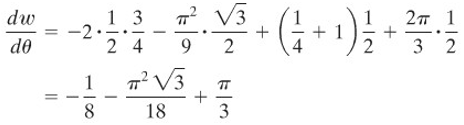
Versi kedua
Andaikan bahwa \(z=f(x,y)\) dengan \(x=x(s,t)\) dan \(y=y(s,t)\). Maka masuk akal untuk menanyakan \(∂z/∂s\) dan \(∂z/∂t\). Kita nyatakan dalam teorema berikut.
Teorema B: Aturan Rantai
Misalkan \(x=x(s,t)\) dan \(y=y(s,t)\) mempunyai turunan pertama di \((s,t)\) dan misalkan \(z=f(x,y)\) dapat didiferensialkan di \((x(s,t),y(s,t))\). Maka \(z=f(x(s,t),y(s,t))\) mempunyai turunan parsial pertama yang diberikan oleh

Contoh 4:
Jika \(z=3x^2-y^2\) dengan \(x=2s+7t\) dan \(y=5st\), tentukan \(∂z/∂t\), dan nyatakan dalam bentuk \(s\) dan \(t\).
Penyelesaian:

Tentu saja, jika kita substitusikan pernyataan \(x\) dan \(y\) ke dalam rumus untuk \(z\) dan kemudian mengambil turunan parsial terhadap \(t\), kita dapatkan jawaban yang sama.
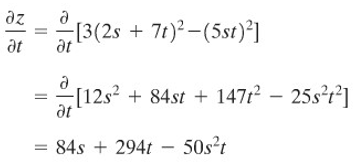
Contoh 5:
Jika \(w=x^2+y^2+z^2+xy\), dengan \(x=st,y=s-t\),dan \(z=s+2t\), tentukan \(∂w/∂t\).
Penyelesaian:

Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
The man who removes a mountain begins by carrying away small stones.
Chinese Proverbs
