www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Integral Lipat Tiga › Integral Lipat Tiga dalam Koordinat Bola - Materi, Contoh Soal dan Pembahasan
Integral Lipat
Integral Lipat Tiga dalam Koordinat Bola - Materi, Contoh Soal dan Pembahasan
Perhitungan integral lipat tiga atas suatu benda pejal S sering kali dipermudah dengan menggunakan koordinat bola. Begitu pula jika S simetri terhadap suatu titik, koordinat bola boleh jadi sangat membantu.
Pada tulisan sebelumnya, kita telah mengetahui bahwa bilamana suatu benda pejal \(S\) di ruang dimensi tiga mempunyai suatu sumbu simetri, perhitungan integral lipat tiga atas \(S\) sering kali dipermudah dengan menggunakan koordinat tabung. Begitu pula jika S simetri terhadap suatu titik, koordinat bola boleh jadi sangat membantu.
Perhatikanlah Gambar 1 yang mengingatkan kita tentang arti dari koordinat bola. Kemudian kita menelaah bahwa persamaan
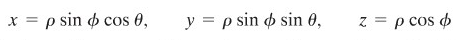
menghubungkan koordinat bola dan koordinat Cartesius.

Gambar 1 (Kiri) dan 2 (Kanan)
Gambar 2 memperlihatkan elemen volume dalam koordinat bola (disebut baji bola). Walaupun kita menghilangkan perinciannya, dapat diperlihatkan bahwa volume baji bola yang ditunjukkan adalah
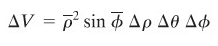
dengan \((\overline{ρ}, \ \overline{θ}, \ \overline{ϕ})\) sebuah titik di baji yang dipilih secara tepat.
Pemartisian suatu benda pejal \(S\) dengan menggunakan suatu kisi bola, yang membentuk jumlah yang cocok, dan dengan mengambil limit akan menghasilkan suatu integral yang mana \(dz \ dy \ dx\) digantikan oleh \(ρ^2 \ \sin ϕ \ dρ \ dθ \ dϕ\).

Contoh 1:
Tentukan volume suatu benda pejal homogen \(S\) yang dibatasi di atas oleh bola \(ρ=a\) dan di bawah oleh kerucut \(∅=α\), dengan \(a\) dan \(α\) konstanta (Gambar 3).
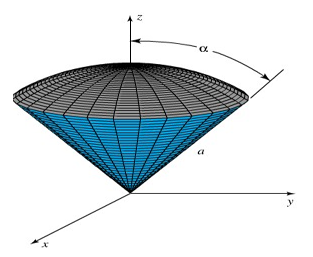
Gambar 3
Penyelesaian:
Volume \(V\) diberikan oleh

Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
The only way to do great work is to love what you do.
Steve Jobs
