www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Fungsi Peubah banyak › Grafik Fungsi Peubah Banyak dengan Kontur
Fungsi
Grafik Fungsi Peubah Banyak dengan Kontur
Sering kali sangat sukar mensketsa permukaan (surface) yang berpadanan dengan grafik dari fungsi dua peubah. Ada cara lain dan biasanya lebih mudah untuk menggambarkan sebuah surface, yang disebut peta kontur.
Sering kali sangat sukar mensketsa permukaan (surface) yang berpadanan dengan grafik dari fungsi dua peubah \(z=f(x,y)\). Pembuat bagan telah memberikan cara lain dan biasanya lebih mudah untuk menggambarkan sebuah permukaan, yang disebut peta kontur.
Setiap bidang mendatar \(z=c\) memotong permukaan dalam bentuk sebuah kurva. Proyeksi kurva pada bidang \(xy\) disebut kurva ketinggian atau level curve (Gambar 1), dan kumpulan lengkungan-lengkungan yang demikian adalah suatu peta kontur. Kita akan memperlihatkan peta kontur untuk sebuah permukaan bentuk bukit pada Gambar 2.

Gambar 1.
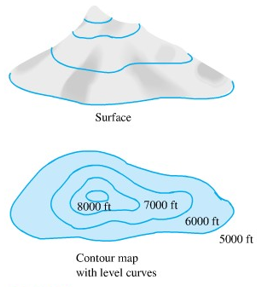
Gambar 2.
Contoh 1:
Gambar peta-peta kontur untuk permukaan yang berpadanan dengan \(z=\frac{1}{3} \sqrt{(36-9x^2-4y^2)}\) dan \(z=y^2-x^2\) (Lihat Gambar 3).
Penyelesaian:

Gambar 3.
Kurva-kurva ketinggian dari \(z=\frac{1}{3} \sqrt{(36-9x^2-4y^2)}\) berpadanan dengan \(z=0,1,1,5,1,75,2\) diperlihatkan pada Gambar 4 (sebelah kiri). Kurva-kurva tersebut adalah elips. Dengan cara yang sama, pada Gambar 4 (sebelah kanan), kita perlihatkan kurva ketinggian dari \(z=y^2-x^2\) untuk \(z=-5,-4,-3,…,2,3,4\). Kurva-kurva ini berbentuk hiperbol.

Gambar 4.
Contoh 2:
Sketsalah peta kontur untuk \(z=f(x,y)=xy\).
Penyelesaian:
Kurva ketinggian yang berpadanan dengan \(z=-4,-1,0,1,4\) diperlihatkan pada Gambar 5. Dapat diperlihatkan bahwa kurva tersebut berbentuk hiperbol.

Gambar 5.
Grafik Komputer dan Level Ketinggian
Pada beberapa gambar berikut, kita telah melukiskan beberapa permukaan beserta dengan level ketinggian yang berpadanan.

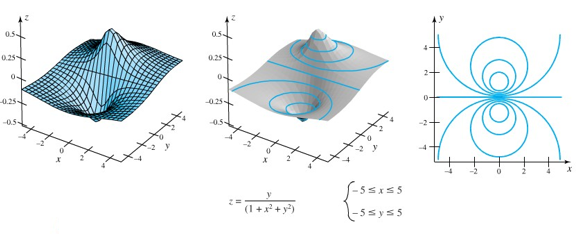
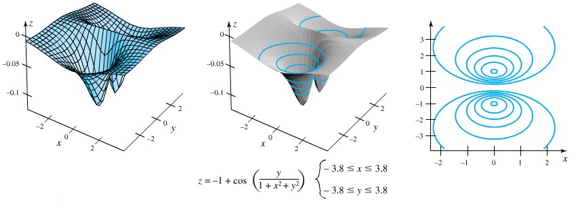


Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
Life is like a camera. Just focus on what’s important, capture the good times, develop from the negatives, and if things don’t work out, just take another shot.
Unknown
