www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Turunan Fungsi Peubah Banyak › Optimasi Fungsi dengan Metode Pengali Lagrange - Materi, Contoh Soal dan Pembahasan
Turunan
Optimasi Fungsi dengan Metode Pengali Lagrange - Materi, Contoh Soal dan Pembahasan
Dalam hidup ini kita akan menjumpai banyak masalah dan kadang kala masalah tersebut dapat dirumuskan sehingga akan melibatkan memaksimumkan atau meminimumkan (nilai ekstrem) fungsi tertentu.
Dalam hidup ini kita akan menjumpai banyak masalah dan kadang kala masalah tersebut dapat dirumuskan sehingga akan melibatkan memaksimumkan atau meminimumkan (nilai ekstrem) fungsi tertentu. Secara umum, masalah tersebut dapat dibedakan menjadi dua yakni masalah nilai ekstrem bebas dan masalah nilai ekstrem terkendala.
Banyak permasalahan di dunia nyata, khususnya di bidang ekonomi, termasuk jenis masalah yang kedua. Sebagai contoh, seorang pengusaha ingin memaksimumkan keuntungan, tetapi dibatasi oleh banyaknya bahan mentah yang tersedia, banyaknya tenaga kerja, dan sebagainya.
Masalah nilai ekstrem bebas (tanpa kendala) telah kita bahas pada artikel sebelumnya. Contohnya adalah ketika kita mencari nilai minimum dari \(x^2+2y^2+z^4+4\). Kita sebut ini sebagai masalah nilai ekstrem bebas karena tidak ada kendala dalam proses pencarian nilai minimum fungsi tersebut.
Ini berbeda dengan masalah nilai ekstrem terkendala yang mana ketika mencari nilai ekstrem suatu fungsi, kita menghadapi kendala tertentu. Sebagai contoh, kita diminta mencari jarak minimum dari permukaan \(z^2=x^2 y+4\) ke titik asal. Kita formulasikan masalah sebagai peminimuman \(d^2=x^2+y^2+z^2\) terhadap kendala \(z^2=x^2 y+4\). Kita tangani masalah tersebut dengan mensubstitusi nilai \(z^2\) dari kendala dalam rumus untuk \(d^2\) dan kemudian menyelesaikan masalah nilai ekstrem bebas yang dihasilkan.
Contoh lain misalnya ketika kita diminta mencari nilai maksimum dan minimum fungsi \(f(x,y)=2+x^2+y^2\) pada himpunan tertutup dan terbatas \(S={(x,y):x^2+1/4 y^2≤1}\). Kita tahu bahwa nilai maksimum muncul pada batas daerah \(S\), sehingga kita diarahkan pada masalah memaksimumkan \(z=2+x^2+y^2\) terhadap kendala \(x^2+1/4 y^2=1\). Masalah ini diselesaikan dengan mencari sebuah parameter untuk kendala tersebut dan kemudian memaksimumkan fungsi satu variabel (variabel yang menjadi parameter dalam kendala).
Namun, sering kali terjadi bahwa persamaan kendala tidak mudah diselesaikan untuk salah satu peubah dan, kendatipun hal ini dapat dikerjakan, boleh jadi terdapat metode lain yang lebih praktis. Ini adalah metode pengali Lagrange, dinamai menurut penemunya yakni Josefph Louis lagrange.
Tafsiran Geometri dari Metode Pengali Lagrange
Bagian masalah dalam Contoh di atas adalah memaksimalkan fungsi objektif \(f(x,y)=2+x^2+y^2\) terhadap kendala \(g(x,y)=0\), di mana \(g(x,y)=x^2+1/4 y^2-1\). Gambar 1 menunjukkan permukaan \(z=f(x,y)\) bersama dengan kendala.
Di sini, elliptical cylinder menyatakan kendala. Bagian kedua dalam Gambar 1 menunjukkan perpotongan kendala dan permukaan \(z=f(x,y)\). Masalah optimisasi adalah mencari di mana, bersama kurva perpotongan ini, fungsi tersebut maksimum dan di mana ia minimum. Baik bagian kedua dan ketiga dalam Gambar 1 menyarankan bahwa nilai maksimum dan minimum akan muncul apabila kurva ketinggian fungsi objektif \(f\) bersinggungan dengan kurva kendala. Ini adalah ide kunci di belakang metode pengali Lagrange.

Gambar 1.
Pertama mari kita pandang kasus di mana kita ingin memaksimumkan atau meminimumkan \(f(x,y)\) terhadap kendala \(g(x,y)=0\). Gambar 1 memberikan saran atau suatu tafsiran geometri dari masalah ini.
Gambar 2.
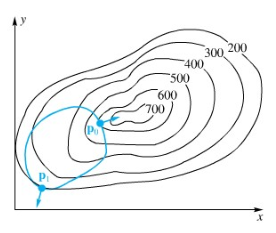
Kurva ketinggian dari \(f\) adalah kurva-kurva \(f(x,y)=k\), dengan \(k\) suatu konstanta. Kurva-kurva tersebut diperlihatkan sebagai kurva-kurva hitam pada Gambar 2 untuk \(k = 200, \ 3000, …,700\). Grafik dari kendala \(g(x,y)=0\) juga berupa sebuah kurva; ia diperlihatkan dalam warna pada Gambar 2.
Untuk memaksimumkan \(f\) terhadap kendala \(g(x,y)=0\) sama dengan mencari kurva ketinggian dengan kemungkinan \(k\) terbesar yang memotong kurva kendala, secara geometri jelas dari Gambar 2 bahwa kurva ketinggian yang demikian menyinggung kurva kendala di suatu titik \(P_0 (x_0,y_0)\) dan karenanya nilai maksimum \(f\) terhadap kendala \(g(x,y)=0\) adalah \(f(x_0,y_0)\). Titik singgung lainnya \(P_1 (x_1,y_1)\) memberikan nilai minimum \(f(x_1,y_1)\) dari \(f\) terhadap kendala \(g(x,y)=0\).
Metode Lagrange menyajikan suatu prosedur aljabar untuk penentuan titik \(P_0\) dan \(P_1\). Karena di titik-titik demikian, kurva ketinggian dan kurva kendala saling menyinggung (yaitu, mempunyai suatu garis singgung bersama), kedua kurva tersebut mempunyai suatu garis tegaklurus bersama. Tetapi di sebarang titik dari kurva ketinggian, vektor gradien \(∇f\) adalah tegaklurus terhadap kurva ketinggian (Pasal 15.5), dan dengan cara serupa \(∇g\) adalah tegaklurus terhadap kurva kendala. Jadi \(∇f\) dan \(∇g\) sejajar di \(P_0\) dan juga di \(P_1\) yaitu

untuk suatu bilangan \(λ_0\) dan \(λ_1\) taknol.
Teorema: Metode Lagrange
Untuk memaksimumkan atau meminimumkan \(f(p)\) terhadap kendala \(g(p)=0\), selesaikan sistem persamaan
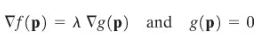
untuk \(p\) dan \(λ\). Tiap titik \(p\) yang demikian adalah suatu titik kritis untuk masalah nilai ekstrem terkendala dan \(λ\) yang berpadanan disebut pengali Lagrange.
Contoh 1:
Berapa luas daerah terbesar yang dapat dimiliki oleh suatu persegi panjang jika panjang diagonalnya 2?
Penyelesaian:
Letakkan persegi panjang itu dikuadran pertama dengan dua sisinya sepanjang sumbu-sumbu koordinat; maka titik sudut yang berhadapan dengan titik asal mempunyai koordinat \((x,y)\), dengan \(x\) dan \(y\) positif (Gambar 3). Panjang diagonalnya adalah \(\sqrt{x^2+y^2}=2\) dan luasnya adalah \(xy\).
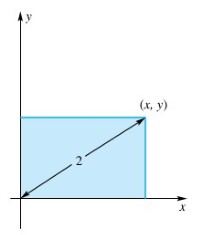
Gambar 3.
Jadi, kita boleh merumuskan masalah berupa pemaksimuman \(f(x,y)=xy\) terhadap kendala \(g(x,y)=x^2+y^2-4=0\). Gradien yang berpadanan adalah
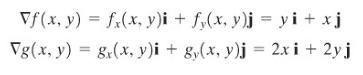
Sekarang persamaan-persamaan Lagrange menjadi

yang mana harus kita selesaikan secara serentak. Jika persamaan pertama kita kalikan dengan \(y\) dan persamaan kedua dengan \(x\), kita peroleh \(y^2=2λxy\) dan \(x^2=2λxy\), yang menghasilkan

Dari (3) dan (4), kita temukan \(x=\sqrt{2}\) dan \(y=\sqrt{2}\); dan dengan mensubstitusi nilai-nilai ini kedalam (1), kita dapatkan \(λ=1/2\). Jadi, penyelesaian persamaan (1) – (3), dengan membuat \(x\) dan \(y\) positif, adalah \(x=\sqrt{2}, \ y=\sqrt{2}, \ λ=1/2\).
Kita simpulkan bahwa persegi panjang yang luasnya terbesar dengan diagonal 2 adalah bujur sangkar, yang panjang sisinya \(\sqrt{2}\). Luasnya adalah 2. Tafsiran geometri masalah ini diperlihatkan pada Gambar 4.

Gambar 4.
Contoh 2:
Gunakan metode Lagrange untuk mencari nilai-nilai maksimum dan minimum dari
\[ f(x,y) = y^2 - x^2 \] pada elips \(x^2/4+y^2=1\).
Penyelesaian:
Lihat ke Gambar 2 dari Pasal 15.8 untuk grafik dari paraboloid hiperbol \(z=f(x,y)=y^2-x^2\). Dari gambar ini, tentu saja kita akan menerka bahwa nilai minimum terjadi di \((±2,0)\) dan nilai maksimum di \((0,±1)\). Tetapi mari kita berikan alasan dugaan ini.
Kita boleh menuliskan kendala sebagai \(g(x,y)=x^2+4y^2-4=0\). Sekarang
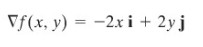
dan

Persamaan-persamaan Lagrange adalah

Perhatikan dari persamaan ketiga bahwa \(x\) dan \(y\) keduanya tidak dapat sama dengan nol. Jika \(x≠0\), persamaan pertama menyimpulkan bahwa \(λ=-1\), kemudian persamaan kedua mensyaratkan bahwa \(y=0\). Kita simpulkan dari persamaan kedua bahwa \(x=±2\). Jadi kita telah memperoleh titik-titik kritis \((±2,0)\).
Argumentasi yang persis sama, dengan y≠0 menghasilkan \(λ=1/4\) dari persamaan kedua, kemudian dari persamaan pertama \(x=0\), dan akhir dari persamaan ketiga \(y=±1\). Kita simpulkan bahwa \((0,±1)\) juga merupakan titik titik kritis.
Sekarang untuk \(f(x,y)=y^2-x^2\),
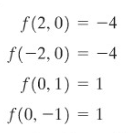
Nilai minimum dari \(f(x,y)\) pada elips yang diberikan adalah -4; nilai maksimum adalah 1.
Contoh 3:
Tentukan minimum \(f(x,y,z)=3x+2y+z+5\), terhadap kendala \(g(x,y,z)=9x^2+4y^2-z=0\).
Penyelesaian:
Gradien \(f\) dan \(g\) adalah \(∇f(x,y,z)=3i+2j+k\) dan \(∇g(x,y,z)=18xi+8yj-k\). Untuk menemukan titik titik kritis, kita pecahkan persamaan-persamaan

untuk \((x,y,z,λ)\) dengan \(λ\) pengali lagrange. Ini setara, dalam soal ini, dengan memecahkan sistem empat persamaan simultan berikut dalam empat peubah \(x, \ y, \ z\), dan \(λ\).

Dari (3), \(λ=-1\). Dengan mensubstitusi hasil ini ke dalam (1) dan (2), kita dapatkan \(x=-1/6\) dan \(y=-1/4\). Dengan memasukkan nilai-nilai ini untuk x dan y dalam persamaan (4), kita peroleh \(z=1/2\). Jadi, penyelesaian sistem empat persamaan simultan tersebut adalah \((-1/6,-1/4,1/2,-1)\), dan satu-satunya titik kritis adalah \((-1/6,-1/4,1/2)\). Maka minimum \(f(x,y,z)\) terhadap kendala \(g(x,y,z)=0\) adalah \(f(-1/6,-1/4,1/2)=4 1/2\). (Bagaimana kita mengetahui bahwa nilai ini lebih tepat minimum ketimbang maksimum)
Dua atau Lebih Kendala
Bilamana ada lebih dari satu kendala yang diberlakukan pada peubah-peubah suatu fungsi yang harus dimaksimumkan atau diminimumkan, maka digunakan pengali-pengali Lagrange tambahan (satu untuk setiap kendala). Misalnya, jika kita mencari ekstrem suatu fungsi \(f\) tiga peubah, terhadap dua kendala \(g(x,y,z)=0\) dan \(h(x,y,z)=0\), kita pecahkan persamaan-persamaan

untuk \(x, y, z, λ\), dan \(μ\), dengan \(λ\) dan \(μ\) adalah pengali-pengali Lagrange. Ini setara terhadap pencarian penyelesaian sistem lima persamaan simultan dalam peubah-peubah \(x, y , z, λ\) dan \(μ\).
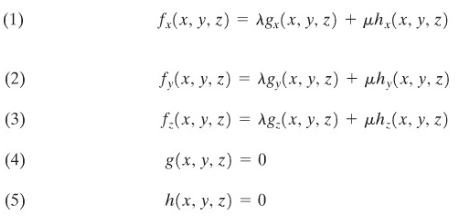
Dari penyelesaian sistem ini kita peroleh titik-titik kritis.
Contoh 4:
Tentukanlah nilai-nilai maksimum dan minimum dari \(f(x,y,z)=x+2y+3z\) pada elips yang merupakan perpotongan tabung \(x^2+y^2=2\) dan bidang \(y + z = 1\) (lihat Gambar 5).
Penyelesaian:
Kita ingin memaksimumkan dan meminimumkan \(f(x,y,z)\) terhadap \(g(x,y,z)=x^2+y^2-2=0\) dan \(h(x,y,z)=y+z-1=0\). Persamaan-persamaan Lagrange yang berpadanan adalah

Dari (1), \(x=1/2λ\); dari (2) dan (3), \(y=-1/2λ\). Jadi, dari (4), \((1/2λ)+(-1/2λ)^2=2\), yang menyimpulkan bahwa \(λ=±1/2\). Jawaban \(λ=1/2\) menghasilkan titik kritis \((x,y,z)=(1,-1,2)\) dan \(λ=-1/2\) menghasilkan titik kritis \((x,y,z)=(-1,1,0)\). Kita simpulkan bahwa \(f(1,-1,2)=5\) adalah nilai maksimum dan \(f(-1,1,0)=1\) adalah nilai minimum.

Gambar 5
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
You can't blame gravity for falling in love.
Albert Einstein
