www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Integral Lipat Dua › Integral Lipat Dua Atas Daerah Persegi Panjang - Materi, Contoh Soal dan Pembahasan
Integral Lipat
Integral Lipat Dua Atas Daerah Persegi Panjang - Materi, Contoh Soal dan Pembahasan
Secara sederhana, integral lipat (integral berulang atau integral ganda) itu adalah integral untuk fungsi lebih dari dua peubah.
Materi integral telah diperkenalkan pada pelajaran matematika dasar dan kalkulus I di website ini. Di sana telah dipelajari konsep mengenai integral terutama untuk fungsi satu peubah dan juga bagaimana menghitung integral untuk berbagai jenis fungsi. Selain itu, kita juga belajar sebuah pendekatan dalam mencari integral menggunakan apa yang disebut integral Riemaan.
Semua penjelasan tersebut akan berguna untuk memahami apa yang akan kita pelajari sekarang dan beberapa artikel selanjutnya terkait integral lipat. Secara sederhana, integral lipat (integral berulang atau integral ganda) itu adalah integral untuk fungsi lebih dari dua peubah. Pada artikel ini, akan dibahas integral lipat dua atas daerah persegi panjang.
Sama seperti pada integral fungsi satu peubah, di sini penjelasan mengenai integral lipat dua akan dimulai dengan integral Riemaan. Ingat bahwa dalam integral Riemaan untuk fungsi satu peubah, kita membentuk suatu partisi \(P\) dari selang \([a, b]\) menjadi beberapa selang bagian yang panjangnya \(Δx_k,k=1,2,…,n\), kemudian mengambil sebuah titik contoh \(\overline{x}_k\) dari selang bagian ke-\(k\), lalu menuliskan

Pahamilah penulisan integral tentu untuk satu peubah di atas, karena kita akan menuliskan dalam cara yang persis sama untuk mendefinisikan integral untuk fungsi dua peubah.
Sekarang perhatikanlah Gambar 1 di bawah ini. Kita tetapkan \(R\) berupa suatu persegi panjang dengan sisi-sisi sejajar sumbu-sumbu koordinat; yakni,


Gambar 1.
Kita mempartisi persegi panjang R dengan memakai sarana berupa garis-garis sejajar sumbu \(x\) dan \(y\) menjadi beberapa persegi panjang kecil , semuanya \(n\) buah, yang kita tunjukkan dengan \(R_k,k=1,2,…,n\). Tetapkan \(Δx_k\) dan \(Δy_k\) adalah panjang sisi-sisi \(R_k\) dan \(ΔA_k=Δx_k Δy_k\) adalah luasnya. Pada \(R_k\), ambil sebuah titik contoh \((\overline{x}_k, \overline{y}_k)\) dan bentuk penjumlahan Riemann

yang berpadanan (jika \(f(x,y) ≥ 0\)) dengan jumlah volume dari \(n\) kotak (Gambar 2 dan 3). Dengan membuat partisi semakin lama semakin halus dengan cara sedemikian sehingga semua \(R_k\) menjadi lebih kecil, maka kita akan akan menuju ke konsep integral lipat dua.

Gambar 2 (Kiri) dan 3 (Kanan).
Setelah penjelasan di atas dipahami, sekarang kita siap untuk sebuah definisi formal. Kita gunakan cara penulisan yang diperkenalkan di atas, dengan ketentuan tambahan bahwa norma dari partisi \(P\) yang dinyatakan oleh \(|P|\) – adalah panjang diagonal terpanjang dari setiap persegi panjang bagian dalam partisi.
Definisi:
Andaikan \(f\) suatu fungsi dua peubah yang terdefinisi pada suatu persegi panjang tertutup \(R\). Jika
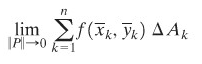
ada, kita katakan \(f\) dapat diintegralkan pada \(R\). Lebih lanjut, \(∬_R f(x,y) \ dA\), yang disebut integral lipat-dua \(f\) pada \(R\), diberikan oleh

Anda mungkin masih ingat dalam pelajaran Kalkulus 1 bahwa jika \(f(x) ≥ 0\), maka \(∫_a^b f(x) \ dx\) menyatakan luas daerah di bawah kurva \(y = f(x)\) antara \(a\) dan \(b\). Dalam cara yang serupa, jika \(f(x,y) ≥ 0\), maka \(∬_R f(x,y) \ dA\) menyatakan volume benda pejal di bawah permukaan \(z = f(x,y)\) dan di atas persegi panjang \(R\) (Gambar 4).

Gambar 4.
Eksistensi Integral Lipat Dua
Tidak setiap fungsi dua peubah dapat diintegralkan pada suatu persegi panjang \(R\) yang diberikan. Alasannya sama seperti pada kasus satu peubah. Dalam hal khusus, suatu fungsi yang tak terbatas pada \(R\) akan selalu tidak dapat diintegralkan. Mari kita simak teorema berikut ini.
Teorema A: Teorema Keterintegralan
Jika \(f\) terbatas pada suatu persegi panjang tertutup \(R\) dan jika ia kontinu di sana, maka \(f\) dapat diintegralkan pada \(R\). Dalam hal khusus, jika \(f\) kontinu pada seluruh \(R\), maka \(f\) dapat diintegralkan di sana.
Sebagai akibatnya, hampir semua fungsi biasa (asalkan mereka terbatas) dapat diintegralkan pada setiap persegi panjang. Misalnya, fungsi berikut

adalah dapat diintegralkan pada setiap persegi panjang. Namun, fungsi

tidak akan dapat diintegralkan pada sebarang persegi panjang yang memotong parabol \(y=x^2\). Kenapa?
Sifat-Sifat Integral Lipat Dua
Integral lipat-dua mewarisi hampir semua sifat-sifat dalam integral tunggal, yakni
- Integral lipat dua bersifat linear, yaitu:
- Integral lipat-dua bersifat aditif pada persegi panjang (Gambar 5) yang saling melengkapi hanya pada suatu ruas garis.
- Sifat pembandingan berlaku. Jika \(f(x,y) ≤ g(x,y)\) untuk semua \((x,y)\) di \(R\), maka



Gambar 5.

Semua sifat-sifat ini berlaku tidak hanya pada himpunan-himpunan berupa persegi panjang, melainkan juga yang bukan persegi panjang. Namun, kita akan membahasnya pada artikel lain untuk itu.
Perhitungan Integral Lipat-Dua
Pertama-tama, perhatikan bahwa jika \(f(x,y)=1\) pada R, maka integral lipat-dua merupakan luas R, dan dari ini menyusul bahwa

Contoh 1:
Andaikan \(f\) berupa fungsi tangga dari Gambar 6 di bawah ini, yakni andaikan


Gambar 6.
Penyelesaian:
Perkenalkan persegipanjang \(R1, R2\), dan \(R3\), sebagai berikut.

Kemudian, dengan menggunakan sifat penjumlahan dari integral lipat-dua, kita peroleh

Contoh 1 di atas merupakan contoh sederhana untuk integral lipat dua. Dalam contoh 2 berikut ini kita akan mengaproksimasi suatu integral lipat dua dengan cara menghitung suatu penjumlahan Riemann sesuai dengan penjelasan kita di atas.
Contoh 2:
Hampiri \(∬_R f(x,y) \ dA\) di mana

dan

Kerjakan ini dengan menghitung penjumlahan Riemann yang diperoleh dengan membagi \(R\) atas delapan bujursangkar yang sama dan dengan menggunakan tiap-tiap pusat bujursangkar sebagai titik contoh (Gambar 7)
Penyelesaian:
Titik-titik contoh yang diperlukan dan nilai-nilai yang berpadanan dari fungsi itu adalah sebagai berikut.


Gambar 7.
Dengan demikian, karena \(ΔA_k=4\), maka

Jadi, nilai hampiran untuk hasil integral lipat dua ini adalah 138.
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
The future belongs to those who believe in the beauty of their dreams.
Eleanor Roosevelt
