Contoh 1:

Tentukan daerah baru yang kita peroleh dengan menerapkan transformasi x = u/2, y = 3v terhadap daerah R yang berupa elips \(x^2+y^2/36=1\).

Pembahasan:

Masukkan transformasi ke dalam persamaan untuk elips. Kita peroleh berikut ini.

Perhatikan bahwa persamaan \(u^2+v^2=4\) merupakan persamaan lingkaran dengan jari-jari 2. Jadi, transformasi ini mengubah daerah berupa elips menjadi sebuah lingkaran yang memiliki jari-jari 2.

Contoh 2:

Tentukan daerah baru yang kita peroleh dengan menerapkan transformasi x = ½ (u + v), y = ½ (u-v) terhadap daerah R yang berupa daerah yang dibatasi oleh y = -x + 4, y = x+1, dan y = x/3 – 4/3.

Pembahasan:

Sama seperti pada Contoh 1, kita perlu memasukkan transformasi ke dalam persamaan. Akan tetapi, dalam kasus ini kita perlu melakukannya tiga kali, yakni sekali untuk masing-masing persamaan. Sebelum kita melakukan itu, kita lukiskan grafik daerah tersebut seperti tampak pada gambar berikut.

Tampak pada gambar di atas bahwa daerah R adalah segitiga. Sekarang, mari kita lakukan transformasi untuk tiap-tiap titik sudut segitiga tersebut.

Untuk y = - x + 4, dengan memasukkan transformasi diperoleh

Perhatikan bahwa transformasi ini menghasilkan persamaan yang jauh lebih sederhana.

Untuk y = x + 1, maka

Sekali lagi, persamaan yang lebih baik diperoleh di sini.

Terakhir, untuk y = x/3 – 4/3. Kita peroleh

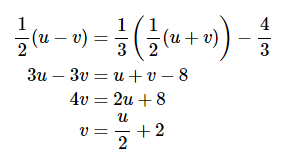
Kita juga peroleh persamaan yang lebih baik di sini, meskipun tidak sebagus pada dua persamaan pertama. Daerah baru yang kita peroleh dari hasil transformasi ini ditampilkan pada gambar berikut

Kita masih peroleh daerah berupa segitiga, namun sebuah segitiga yang jauh lebih baik.