Kalkulus 2 › Integral Lipat Dua › Soal Integral Lipat Dua dalam Koordinat Polar

Integral Lipat Dua

Soal Integral Lipat Dua dalam Koordinat Polar

Dalam teori peluang dan statistika, kita membahas fungsi kepadatan peluang (probability density function) normal standar yaitu

Syarat dari fungsi tersebut yakni \( \int_\limits{-∞}^∞ f(x) \ dx=1\). Buktikanlah bahwa integral tersebut sama dengan 1 sehingga syarat dari fungsi tersebut terpenuhi!

Pembahasan:

Kita akan membuktikan bahwa integral tersebut sama dengan 1 dengan menggunakan integral lipat dua dalam koordinat polar. Kita mulai dengan membuktikan terlebih dahulu integral yang berikut ini

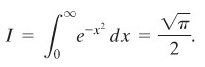
Pertama ingat kembali bahwa

Sekarang andaikan \(V_b\) adalah volume benda pejal (Gambar 1) yang terletak di bawah permukaan \(z=e^{-x^2-y^2}\) dan di atas bujursangkar dengan titik-titik sudut \((±b,±b)\). Maka,

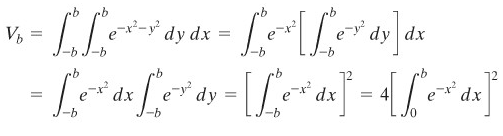
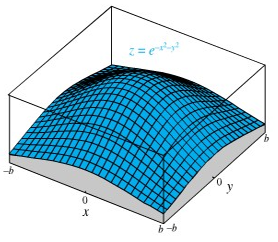
Gambar 1

Ternyata bahwa volume daerah di bawah \(z=e^{-x^2-y^2}\) dan di atas seluruh bidang \(xy\) adalah

Dalam hal lain, kita juga dapat menghitung \(V\) dengan memakai koordinat kutub.Di sini \(V\) adalah limit untuk \(a→∞\) dari \(V_a\), yaitu volume benda pejal di bawah permukaan \(z=e^{-x^2-y^2}=e^{-r^2}\) dan di atas daerah melingkar yang beradius \(a\), berpusat di titik asal. (Gambar 2).

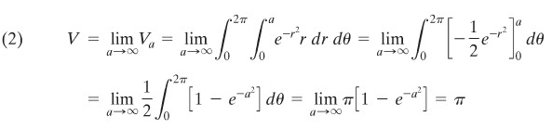
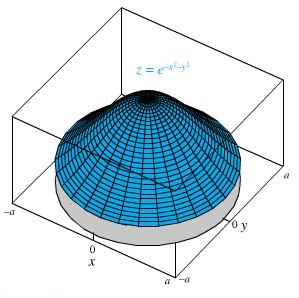
Gambar 2

Penyamaan kedua nilai yang diperoleh untuk \(V\) dalam (1) dan (2) menghasilkan \(4I^2=π\), atau \(I=1/2 \sqrt{π}\), seperti yang diinginkan.

Sekarang kita siap untuk membuktikan fungsi pdf normal baku seperti yang diminta dalam soal. Menurut kesimetrisan,

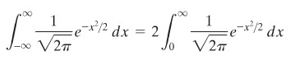
Selanjutnya kita membuat substitusi \(u=x/\sqrt{2}\), sehingga \(dx=\sqrt{2} \ du\). Batas atas dan batas bawah pada integral tetap sama, sehingga kita peroleh

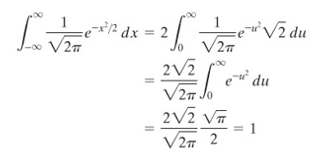
untuk memperoleh baris terakhir, kita gunakan hasil pada pada pembuktian pertama di atas. Dengan demikian, hasil integral tersebut sama dengan 1 yang mana sesuai dengan yang ingin dibuktikan yakni,

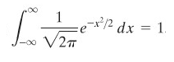
Sumber:

Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.