Aljabar Linear › Nilai Eigen dan Vektor Eigen › Latihan Soal dan Pembahasan Nilai Eigen dan Vektor Eigen Bagian 1

Nilai Eigen dan Vektor Eigen

Latihan Soal dan Pembahasan Nilai Eigen dan Vektor Eigen Bagian 1

Guna memperdalam pemahaman tentang nilai eigen dan vektor eigen (eigen value and vector eigen), berikut ini diberikan sejumlah latihan soal terkait materi tersebut beserta pembahasannya.

Diketahui suatu matriks 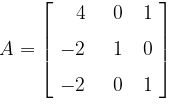. Carilah:

1. Persamaan akar ciri dari matriks A
2. Nilai-nilai akar ciri dari matriks A
3. Vektor-vektor ciri dari matriks A

(Ujian Akhir Semester Aljabar Linear Tahun 2012-2013)

Pembahasan:

a. Menentukan persamaan akar ciri matriks A.

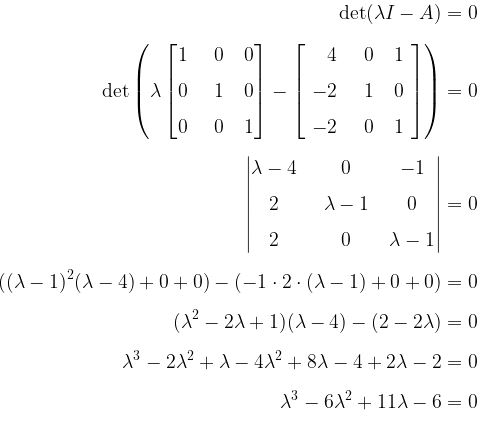
b. Mencari nilai-nilai akar ciri dari matriks A.

Nilai-nilai akar ciri dari matriks A dapat diperoleh dengan mencari akar-akar persamaan kubik yang telah kita peroleh di atas, yakni

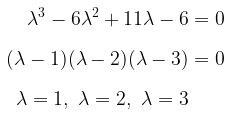
c. Mencari vektor-vektor ciri dari matriks A.

Untuk \( \lambda = 1 \),

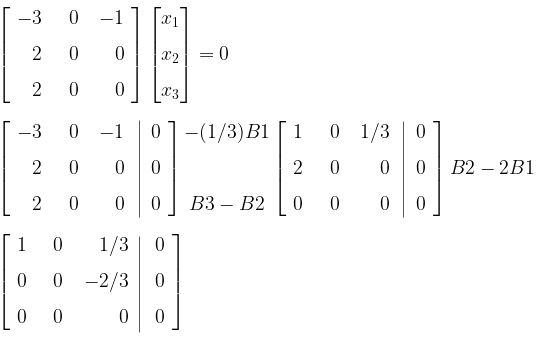
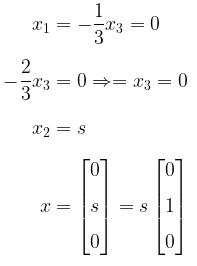
Jadi, vektor ciri untuk \( \lambda = 1 \) adalah \( \begin{bmatrix} 0 \\[8pt] 1 \\[8pt] 0 \end{bmatrix} \).

Untuk \( \lambda = 2 \),

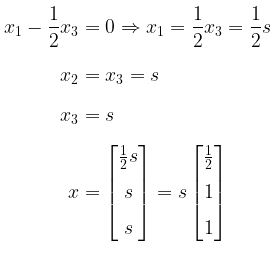
Jadi, vektor ciri untuk \( \lambda = 2 \) adalah \( \begin{bmatrix} \frac{1}{2} \\[8pt] 1 \\[8pt] 1 \end{bmatrix} \).

Untuk \( \lambda = 3 \),

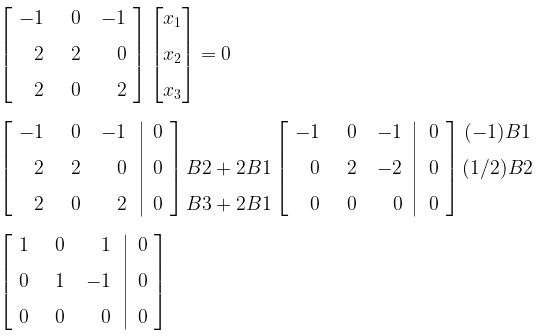
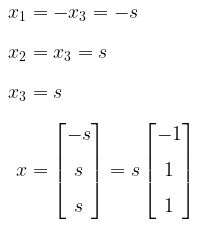
Jadi, vektor ciri untuk \( \lambda = 3 \) adalah \( \begin{bmatrix} -1 \\[8pt] 1 \\[8pt] 1 \end{bmatrix} \).

Dengan demikian, vektor-vektor ciri untuk matriks A adalah \( \begin{bmatrix} 0 \\[8pt] 1 \\[8pt] 0 \end{bmatrix} \) untuk \( \lambda = 1 \), \( \begin{bmatrix} \frac{1}{2} \\[8pt] 1 \\[8pt] 1 \end{bmatrix} \) untuk \( \lambda = 2 \) dan \( \begin{bmatrix} -1 \\[8pt] 1 \\[8pt] 1 \end{bmatrix} \) untuk \( \lambda = 3 \).