Aljabar Linear   »   Sistem Persamaan Linear   ›  Matriks yang Diperbesar (Augmented Matrix)

Matriks yang Diperbesar (Augmented Matrix)

Bila kita membentuk sebuah matriks yang diperbesar (augmented matrix), maka bilangan-bilangan tak diketahui harus dituliskan dalam urutan (orde) yang sama dalam masing-masing persamaan.

Ketika jumlah persamaan dan variabel yang tidak diketahui dalam sistem linier meningkat, demikian juga kompleksitas aljabar yang terlibat dalam menemukan solusi. Komputasi yang diperlukan dapat dibuat lebih mudah dikelola dengan menyederhanakan notasi dan prosedur standarisasi.

Misalnya, sebuah sistem umum yang terdiri dari \(m\) persamaan linear dengan \(n\) bilangan yang tak diketahui akan kita tulis sebagai

Penulisan tikalas ganda pada koefisien bilangan tak diketahui adalah sebuah alat yang berguna yang akan kita terapkan untuk menyatakan letak koefisien dalam sistem tersebut. Tikalas pertama pada koefisien \(a_{ij}\) menunjukkan persamaan yang muncul pada koefisien tersebut, sedangkan tikalas kedua menunjukkan bilangan tak diketahui yang dikalikan oleh koefisien tersebut. Jadi, \(a_{12}\) terdapat pada persamaan pertama dan mengalikan bilangan tak diketahui \(x_2\).

Jika kita telusuri letak \(+\), letak \(x\), dan letak \(=\), maka sistem yang terdiri dari \(m\) persamaan linear dengan \(n\) bilangan tak diketahui dapat disingkat dengan hanya menuliskan jajaran empat persegi panjang dari bilangan-bilangan:

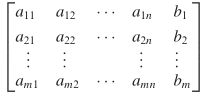
Jajaran ini kita namakan matriks yang diperbesar (augmented matrix) untuk sistem tersbut. Untuk melukiskannya, maka matriks yang diperbesar untuk sistem persamaan-persamaan

adalah

Bila kita membentuk sebuah matriks yang diperbesar, maka bilangan-bilangan tak diketahui harus dituliskan dalam urutan (orde) yang sama dalam masing-masing persamaan.

Sumber:

Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.