Aljabar Linear   »   Matriks   ›  Definisi, Notasi, dan Macam-macam Matriks

Definisi, Notasi, dan Macam-macam Matriks

Sebuah matriks adalah susunan segi empat siku-siku dari bilangan-bilangan. Bilangan-bilangan dalam susunan tersebut dinamakan entri dalam matriks.

Dalam matematika, konsep matriks mempunyai peranan penting terutama berkaitan dengan sistem persamaan linear. Konsep matriks juga sering dijumpai dalam disiplin ilmu lain seperti statistika, ekonomi, sosial, komputer, dan lainnya.

Definisi dan Notasi Matriks

Mari kita mulai dengan definisi mengenai matriks berikut ini.

Sebagai contoh, susunan berikut adalah matriks.

Matriks-matriks yang diberikan dalam contoh ini mempunyai ukuran yang berbeda-beda. Ukuran matriks dinyatakan menurut banyaknya baris (garis horisontal) dan banyaknya kolom (garis vertikal) yang terdapat dalam matriks tersebut. Misalnya, matriks yang pertama dalam contoh ini mempunyai 3 baris dan 2 kolom sehingga ukurannya adalah 3 kali 2 (yang dituliskan 3 x 2).

Angka pertama selalu menunjukkan banyaknya baris dan angka kedua menunjukkan banyaknya kolom. Jadi, matriks lainnya di atas berturut-turut mempunyai ukuran 1 x 4, 3 x 3, 2 x 1, dan 1 x 1. Matriks terakhir adalah berukuran 1 x 1, dan kita sering hanya menuliskan 4 saja ketimbang [4] dan cara penulisan ini merupakan praktek yang sudah umum.

Dalam penulisan matriks, kita akan menggunakan huruf-huruf besar untuk menyatakan matriks-matriks dan menggunakan huruf-huruf kecil untuk menyatakan elemen-elemen atau entri-entri yang ada pada sebuah matriks; jadi, kita dapat menuliskan

Jika \(A\) adalah sebuah matriks, maka kita akan menggunakan \(a_{ij}\) untuk menyatakan entri yang terdapat di dalam baris \(i\) dan kolom \(j\) dari \(A\). Jadi sebuah matriks \(3×4\) yang umum dapat dituliskan sebagai

Demikian pula, jika kita gunakan \(B\) untuk menyatakan matriks, maka kita akan menggunakan \(b_{ij}\) untuk entrinya dalam baris \(i\) dan kolom \(j\). Jadi, matriks \(m×n\) yang umum dapat dituliskan sebagai

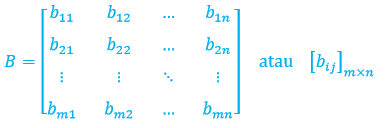
Sebuah matriks dengan \(n\) baris dan \(n\) kolom dinamakan matriks persegi atau matriks kuadrat berordo \(n\) (square matrix of order n), dan entri-entri \(a_{11}, a_{22},\dotsc, a_{nn}\) merupakan diagonal utama dari \(A\) (lihat matriks di bawah).

Macam-macam Matriks

Secara umum, matriks-matriks dapat dibedakan berdasarkan elemen-elemen penyusunnya dan berdasarkan ordo dari matriks tersebut. Berdasarkan elemen-elemen penyusunnya, matriks dapat dibedakan menjadi matriks diagonal, matriks skalar, matriks segitiga bawah, matriks segitiga atas, matriks identitas, matriks nol, matriks simetris, dan matriks transpos.

Sedangkan berdasarkan ordo-nya, matriks dapat dibedakan menjadi matriks bujur sangkar atau matriks persegi/kuadrat, matriks baris, matriks kolom, matriks tegak, matriks datar.

Kita akan menjelaskan secara sekilas matriks-matriks tersebut berikut ini.

Matriks Berdasarkan Elemen-elemen Penyusunnya

1. Matriks diagonal

Matriks Diagonal, yaitu matriks bujur sangkar dengan elemen di luar diagonal utama adalah nol, yaitu \(a_{ij} = 0\) untuk i ≠ j. Sebagai contoh, matriks

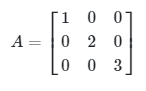
adalah matriks diagonal dengan diagonal utamanya adalah 1, 2, dan 3.

2. Matriks skalar

Matriks Skalar, yaitu matriks diagonal dengan elemen pada diagonal utama adalah sama, yaitu \(a_{ij} = c\) untuk \(i=j\) dan \(a_{ij} = 0\) untuk \(i≠j\). Contoh matriks ini yaitu

3. Matriks segitiga atas

Matriks segitiga atas, yaitu matris bujur sangkar dengan elemen di bawah diagonal utama adalah nol. Contoh:

4. Matriks segitiga bawah

Matriks segitiga bawah, yaitu matriks bujur sangkar dengan elemen di atas diagonal utama adalah nol. Contoh:

5. Matriks identitas

Matriks identitas, yaitu matriks diagonal dengan elemen pada diagonal utama adalah 1, yaitu \(a_{ij} = 1\) untuk \(i=j\) dan \(a_{ij} = 0\) untuk \(i≠j\). Contoh:

6. Matriks Nol

Matriks nol, yaitu matriks yang seluruh elemennya adalah nol. Contoh:

7. Matriks Simetris

Matriks simetris adalah matriks persegi yang setiap elemen pada segitiga atasnya merupakan simetri/pencerminan dari elemen pada segitiga bawah (dicerminkan terhadap diagonal utama). Transpose dari matriks simetris adalah dirinya sendiri. Contoh:

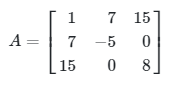
8. Matriks Transpos

Matriks transpos, adalah matriks yang diperoleh dengan menukarkan elemen pada baris menjadi elemen pada kolom. Matriks transpos dinotasikan dengan \(A^T\). Sebagai contoh, jika matriks

maka, matriks transpose nya adalah:

Matriks Berdasarkan Ordo-nya

1. Matriks Bujur Sangkar/Persegi

Matriks bujur sangkar atau matriks persegi adalah matriks yang banyaknya baris sama dengan banyaknya kolom. Contoh:

2. Matriks Baris

Matriks baris adalah matriks yang hanya terdiri dari 1 baris saja. Contoh:

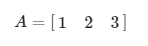
3. Matriks Kolom

Matriks kolom adalah matriks yang hanya terdiri dari 1 kolom saja. Contoh:

4. Matriks Tegak

Matriks tegak adalah matriks yang banyaknya baris lebih besar dari banyaknya kolom. Contoh:

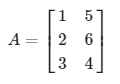
5. Matriks Datar

Matriks Datar adalah matriks yang banyaknya baris kurang dari jumlah kolomnya. Contoh:

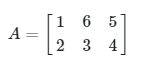
Sumber:

Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.