www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Sistem Persamaan Linear › Sistem Persamaan Linier
Sistem Persamaan Linier
Tidak semua sistem persamaan linear mempunyai pemecahan. Sebuah sistem persamaan yang tidak mempunyai pemecahan dikatakan tak konsisten (inconsistent). Jika ada setidak-tidaknya satu pemecahan, maka sistem persamaan tersebut dinamakan konsisten (consistent).
Sebuah garis dalam bidang \(xy\) secara aljabar dapat dinyatakan oleh persamaan yang berbentuk

Persamaan semacam ini kita namakan persamaan linear dalam peubah (variabel) \(x\) dan peubah \(y\). Secara lebih umum, kita mendefinisikan persamaan linear dalam n peubah \(x_1, x_2,…, x_n\) sebagai persamaan yang dapat dinyatakan dalam bentuk
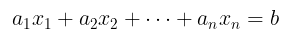
di mana \(a_1, a_2,…, a_n\) dan \(b\) adalah konstanta-konstanta riil.
Contoh 1:
Berikut ini kita berikan persamaan-persamaan linear:
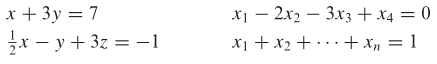
Perhatikanlah bahwa persamaan linear tidak melibatkan suatu hasil kali atau akar peubah dan tidak muncul berupa fungsi trigonometri, fungsi logaritma, atau fungsi eksponsial. Berikut ini bukanlah persamaan linear:

Pemecahan persamaan linear \(a_1x_1 + a_2x_2 + \dots + a_nx_n = b\) adalah urutan dari \(n\) bilangan \(s_1, s_2,…, s_n\) sehingga persamaan tersebut dipenuhi bila kita mensubstitusikannya terhadap \(x_1 =s_1, x_2=s_2,…, x_n=s_n\). Himpunan semua pemecahan persamaan tersebut dinamakan himpunan pemecahannya.
Contoh 2:
Carilah himpunan pemecahan masing-masing persamaan berikut:

Pembahasan:
Untuk mencari pemecahan-pemecahan persamaan (i), maka kita dapat menetapkan sebarang nilai untuk \(x\) dan memecahkan persamaan tersebut untuk mencari \(y\), atau sebaliknya kita dapat memilih sebarang nilai untuk \(y\) dan memecahkan persamaan tersebut untuk mencari \(x\). Jika kita ikuti pendekatan pertama dan menetapkan nilai sebarang \(t\) untuk \(x\), maka kita dapatkan

Rumus-rumus ini menggambarkan himpunan pemecahan tersebut dalam sebarang parameter \(t\). Untuk memperoleh pemecahan khusus, kita dapat mensubstitusikan nilai-nilai spesifik untuk \(t\). Misalnya, \(t = 3\) menghasilkan pemecahan \(x = 3, y = 11/2\) dan \(t = -1/2\) menghasilkan pemecahan \(x = -1/2, y = -3/2\).
Untuk mencari himpunan pemecahan persamaan (ii) kita dapat menetapkan sebarang nilai untuk kedua peubah dan memecahkan persamaan tersebut untuk mencari peubah ketiga. Khususnya, jika kita menetapkan nilai sebarang \(s\) dan \(t\) berturut-turut untuk \(x_2\) dan \(x_3\) dan memecahkan persamaan tersebut untuk mencari \(x_1\), maka kita peroleh
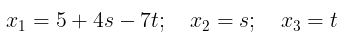
Sistem persamaan linier
Sebuah sistem sebarang yang terdiri dari \(m\) persamaan linear dengan \(n\) bilangan tak diketahui akan dituliskan sebagai

di mana \(x_1, x_2,…, x_n\) adalah bilangan-bilangan tak diketahui sedangkan \(a\) dan \(b\) menyatakan konstanta-kontanta.
Misalnya, sebuah sistem umum yang terdiri dari tiga persamaan linear dengan empat bilangan yang tak diketahui akan kita tulis sebagai

Sebuah himpunan berhingga dari persamaan-persamaan linear dalam peubah \(x_1, x_2,…, x_n\) dinamakan sistem persamaan linear atau sistem linear. Sebuah urutan bilangan-bilangan \(s_1, s_2,…, s_n\) dinamakan pemecahan dari sistem tersebut jika \(x_1 =s_1, x_2=s_2,…, x_n=s_n\) adalah pemecahan masing-masing persamaan pada sistem tersebut. Misalnya, sistem
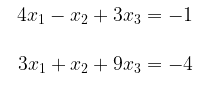
mempunyai pemecahan \(x_1 = 1, x_2 = 2, x_3 = -1\) karena nilai-nilai ini memenuhi kedua persamaan tersebut. Akan tetapi, \(x_1 = 1, x_2 = 8, x_3 = 1\) bukanlah sebuah pemecahan karena nilai-nilai ini hanya memenuhi persamaan pertama dari kedua persamaan dalam sistem tersebut.
Tidak semua sistem persamaan linear mempunyai pemecahan. Perhatikan sistem persamaan linear dua variabel berikut.

Jika kita mengalikan persamaan kedua dari sistem dengan ½, maka jelaslah bahwa tidak ada pemecahan, karena kedua persamaan dalam sistem yang dihasilkan, yakni

bertentangan satu sama lain.
Sebuah sistem persamaan yang tidak mempunyai pemecahan dikatakan takkonsisten (inconsistent). Jika ada setidak-tidaknya satu pemecahan, maka sistem persamaan tersebut dinamakan konsisten (consistent). Untuk melukiskan kemungkinan-kemungkinan yang dapat terjadi dalam memecahkan sistem persamaan linear, tinjaulah sistem umum dari dua persamaan linear dalam bilangan-bilangan yang tak diketahui \(x\) dan \(y\);

Grafik persamaan-persamaan ini merupakan garis-garis; namakanlah garis-garis tersebut \(l_1\) dan \(l_2\). Karena titik \((x,y)\) terletak pada sebuah garis jika dan hanya jika bilangan-bilangan \(x\) dan \(y\) memenuhi persamaan garis tersebut, maka pemecahan sistem persamaan tersebut akan bersesuaian dengan titik perpotongan dari garis \(l_1\) dan \(l_2\). Ada tiga kemungkinan (Gambar 1):
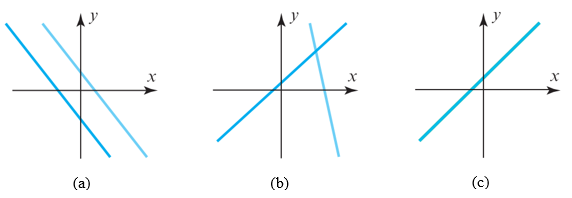
Gambar 1. (a) Tidak ada pemecahan. (b) Satu pemecahan. (c) Takterhingga banyaknya pemecahan
- Garis \(l_1\) sejajar dengan garis \(l_2\) atau tidak ada perpotongannya, dan sebagai konsekuensinya maka tidak ada pemecahan untuk sistem tersebut.
- Garis \(l_1\) berpotongan dengan garis \(l_2\) di hanya satu titik; dalam kasus ini maka sistem tersebut hanya mempunyai satu pemecahan.
- Garis \(l_1\) berimpit dengan garis \(l_2\); dalam kasus ini ada tak terhingga banyaknya titik perpotongan, dan sebagai konsekuensinya maka terdapat tak terhingga banyaknya pemecahan untuk sistem tersebut.
Walaupun di sini kita hanya meninjau dua persamaan dengan dua bilangan tak diketahui, namun hasil yang sama berlaku untuk sebarang sistem dengan tiga kemungkinan yang dapat diperoleh yakni sistem persamaan linear tidak mempunyai pemecahan, atau mempunyai satu pemecahan, atau mempunyai tak terhingga banyaknya pemecahan.
Bentuk Matriks dari Sistem Persamaan Linear
Perkalian matriks mempunyai penerapan penting terhadap sistem persamaan linear. Tinjaulah suatu sistem yang terdiri dari \(m\) persamaan linear dalam \(n\) bilangan tak diketahui.

Karena dua matriks dinyatakan sama jika dan hanya jika entri-entri yang bersesuaian sama, maka kita dapat menggantikan \(m\) persamaan dalam sistem ini dengan persamaan matriks tunggal,
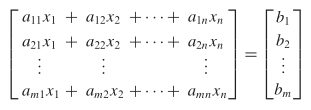
Matriks \(m × 1\) pada ruas kiri persamaan ini dapat dituliskan sebagai hasil kali yang memberikan

Jika kita tandai matriks-matriks ini berturut-turut dengan A, X, dan B, maka sistem \(m\) persamaan asli dalam \(n\) bilangan tak diketahui telah digantikan oleh persamaan matriks tunggal, yakni

Matriks \(A\) dalam persamaan (1) di atas dinamakan matriks koefisien (coefficient matrix) untuk sistem tersebut. Sebagian pekerjaan kita kelak akan diperuntukkan untuk memecahkan persamaan matriks seperti ini terhadap matriks \(X\) tak diketahui. Sebagai konsekuensi pendekatan matriks ini, maka kita akan mendapatkan metode baru yang efektif untuk memecahkan sistem-sistem persamaan linear.
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Mistakes are the portals of discovery.
