www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Vektor & Ruang Vektor › Kebebasan Linear Vektor: Materi, Contoh Soal dan Pembahasan
Kebebasan Linear Vektor: Materi, Contoh Soal dan Pembahasan
Sekelompok vektor disebut bebas linear (linearly independent) apabila masing-masing vektor tersebut tidak dapat ditulis sebagai kombinasi linear dari vektor-vektor yang lain.
Bebas linear merupakan salah satu syarat yang harus dipenuhi oleh suatu himpunan untuk menjadi basis ruang vektor.
Dalam aljabar linear, sekelompok vektor disebut bebas linear (linearly independent) apabila masing-masing vektor tersebut tidak dapat ditulis sebagai kombinasi linear dari vektor-vektor yang lain. Sekelompok vektor yang tidak memenuhi syarat ini dinamakan bergantung linier (linearly dependent). Kita nyatakan definisinya sebagai berikut.
Definisi:
Jika \(S = {v_1, v_2,…, v_r}\) adalah himpunan vektor, maka persamaan vektor

mempunyai paling sedikti satu pemecahan, yakni

Jika ini adalah satu-satuya pemecahan, maka \(S\) kita namakan himpunan bebas linear (linearly independent). Jika ada pemecahan lain, maka \(S\) kita namakan himpunan tak bebas linear (linearly dependent).
Teorema:
Himpunan \(S\) dengan dua vektor atau lebih adalah
- Tak bebas linear jika dan hanya jika paling tidak satu diantara vektor \(S\) dapat dnyatakan sebagai kombinasi linear dari vektor \(S\) lainnya.
- Bebas linear jika dan hanya jika tidak ada vektor \(S\) yang dapat dinyatakan sebagai kombinasi linear dalam vektor \(S\) lainnya.
Teorema:
- Jika sebuah himpunan mengandung vektor nol, maka himpunan itu takbebas linear.
- Sebuah himpunan mempunyai persis dua vektor takbebas linear jika dan hanya jika salah satu dari vektor itu adalah perkalian dari skalar lainnya.
Contoh 1:
Periksa apakah himpunan \(S=\{(1,2),(2,5)\}\) bebas linear dalam ruang vektor \(\mathbb{R}^2\).
Pembahasan:
Perhatikan bahwa (1,2) bukan kelipatan skalar dari (2,5) dan begitupun sebaliknya. Dengan demikian, berdasarkan teorema di atas, maka himpunan \(S\) adalah bebas linear.
Contoh 2:
Tinjaulah vektor-vektor \(i = (1, 0, 0), j = (0, 1, 0) \) dan \(k = (0, 0, 1)\) pada \(R^3\). Perlihatkan bahwa himpunan vektor-vektor tersebut saling bebas linear.
Pembahasan:
Vektor-vektor tersebut saling bebas linear jika persamaan
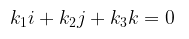
hanya dipenuhi oleh \( k_1 = k_2 = k_3 = 0 \) atau secara ekivalen menjadi
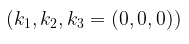
Perhatikan bahwa \(k_1 = 0, k_2 = 0, k_3 = 0\); sehingga himpunan \(S = (i, j, k)\) bebas linear. Uraian serupa dapat digunakan untuk memperlihatkan bahwa vektor-vektor \(e_1 = (1, 0, 0,…, 0), e_2 = (0, 1, 0,…, 0),…, e_n = (0, 0, 0,…, 1)\) membentuk himpunan bebas linear pada \(R^n\).
Contoh 3:
Tentukanlah apakah vektor-vektor

membentuk himpunan takbebas linear atau himpunan bebas linear.
Pembahasan:
Kebebasan linear atau ketidakbebasan linear dari vektor-vektor ini ditentukan oleh persamaan vektor:

Kita tulis ulang dalam bentuk komponen:

Dengan menyamakan komponen yang bersesuaian akan memberikan
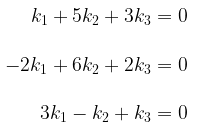
Jadi, \(v_1, v_2\), dan \(v_3\) membentuk himpunan takbebas linear jika sistem ini mempunyai pemecahan takrivial, atau membentuk himpunan bebas linear jika sistem tersebut hanya mempunyai pemecahan trivial. Dengan memecahkan sistem ini maka akan menghasilkan
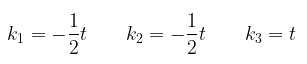
Karena sistem tersebut mempunyai pemecahan taktrivial maka \(v_1, v_2\), dan \(v_3\) membentuk himpunan tak bebas linear.
Karena kita telah menetapkan bahwa vektor \(v_1, v_2\), dan \(v_3\) adalah takbebas linear, maka setidaknya salah satu dari vektor-vektor tersebut adalah kombinasi linear dari yang lain. Seperti yang bisa dilihat, vektor \( v_3 \) adalah kombinasi linear dari vektor \( v_1 \) dan \( v_2 \).
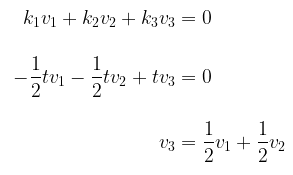
Pada Contoh 3 di atas, secara alternatif, kita bisa menunjukkan adanya pemecahan taktrivial tanpa memecah sistem tersebut dengan memperlihatkan bahwa matriks koefisien mempunyai determinan nol dan sebagai konsekuensinya maka matriks koefisien tersebut tidak dapat dibalik.
Teorema:
Misalkan A adalah matriks persegi. Persamaan \( A\vec{x} = \vec{0} \) hanya mempunyai solusi trivial jika dan hanya jika \( \det A \neq 0 \).
Contoh 4:
Diketahui \(\vec{v}_1=(1,1,2)\), \(\vec{v}_2=(1,0,1)\), dan \(\vec{v_3}=(2,1,3)\). Periksa apakah \(S=\{ \vec{v}_1, \vec{v}_2, \vec{v_3} \}\) bebas linear dalam ruang vektor \(\mathbb{R}^3\).
Pembahasan:
Untuk menentukan himpunan \(S\) bebas linear atau tidak, perlu diperiksa apakah persamaan

hanya dipenuhi oleh \(k_1=k_2=k_3=0\). Perhatikan bahwa
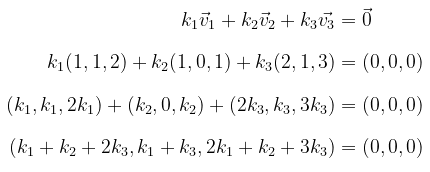
Berdasarkan kesamaan vektor pada \(\mathbb{R}^3\), diperoleh
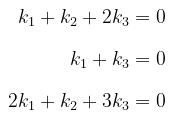
Matriks koefisien dari sistem persamaan di atas adalah

Determinan dari matriks A adalah nol yakni
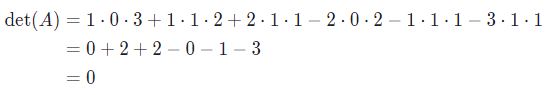
Dengan demikian, persamaan (1) mempunyai solusi non trivial. Akibatnya, himpunan \( S \) bergantung linear.
Dalam \(R^2\) atau \(R^3\), satu vektor adalah kelipatan skalar dari vektor lainnya jika dan hanya jika kedua vektor yang terletak pada garis yang sama yang melalui titik asal ditempatkan pada titik awalnya melalui titik asal. Jadi, dalam \(R^2\) atau \(R^3\) dua vektor yang berbentuk himpunan takbebas linear adalah jika dan hanya jika vektor itu terletak pada garis yang sama melalui titik asal yang ditempatkan pada titik awalnya melalui titik asal itu sendiri. Lihat Gambar 1 berikut.
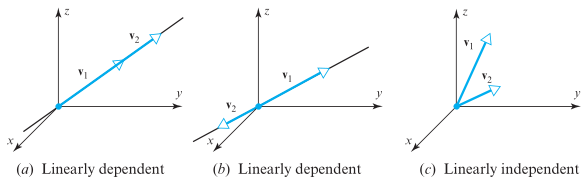
Gambar 1.
Jika \(v_1, v_2\), dan \(v_3\) adalah tiga vektor pada \(R^3\), maka himpunan \(S=\{v_1, v_2,v_3\}\) takbebas linear jika dan hanya jika ketiga vektor tersebut terletak pada bidang yang sama melalui titik asal bila vektor-vektor tersebut ditempatkan dengan titik-titik awalnya di titik asal (lihat Gambar 2).

Gambar 2.
Himpunan bebas linear pada Rn dapat mengandung paling banyak \(n\) vektor. Kita nyatakan dalam teorema berikut.
Teorema:
Misalkan \(S=\{v_1, v_2,…, v_r\}\) adalah himpunan vektor-vektor pada \(R^n\). Jika \(r > n\), maka \(S\) takbebas linear.
Bukti:
Misalkan

Tinjaulah persamaan

Jika kita menyatakan kedua ruas dari persamaan ini dalam komponen-komponennya dan kemudian menyamakan komponen-komponen yang bersesuaian, kita dapatkan sistem
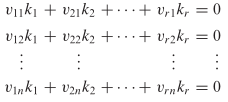
Ini merupakan sistem homogen dari \(n\) persamaan pada \(r\) bilangan tak diketahui \(k_1,…, k_r\). Karena \(r > n\), maka sistem tersebut mempunyai pemecahan taktrivial. Jadi, \(S=\{v_1, v_2,…, v_r\}\) adalah himpunan tak bebas linear.
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
If you spend your whole life waiting for the storm, you’ll never enjoy the sunshine.
