Contoh 1: Rentang

Vektor-vektor \(i = (1, 0, 0), j = (0, 1, 0)\), dan \(k = (0, 0, 1)\) merentang \(R^3\) karena setiap vektor \((a, b, c)\) pada \(R^3\) dapat kita tuliskan sebagai

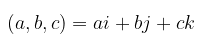
Contoh 2: Rentang

Tentukan apakah \(v_1 = (1, 2, 3), v_2 = (1, 4, 6)\), dan \(v_3 = (2, -3, -5)\) merentangkan ruang vektor \(R^3\).

Pembahasan:

Kita harus menentukan apakah sebarang vektor \(b = (b_1, b_2, b_3)\) di \(R^3\) dapat dinyatakan sebagai kombinasi linear dari vektor \(v_1, v_2\), dan \(v_3\) dalam bentuk persamaan:

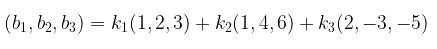
Penyamaan komponen-komponen yang bersesuaian memberikan

Selanjutnya adalah kita perlu menentukan apakah sistem persamaan linier di atas mempunyai solusi untuk semua nilai \(b = (b_1, b_2, b_3)\). Sistem persamaan linier nonhomogen di atas akan konsisten atau mempunyai solusi apabila matriks koefisiennya memiliki determinan bukan nol.

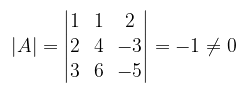
Karena determinan \(A = -1\), maka sistem persamaan linier di atas konsisten atau memiliki solusi, sehingga dapat dibuat kombinasi linier dari \(v_1, v_2\), dan \(v_3\). Karena itu dikatakan \(v_1, v_2\), dan \(v_3\) merentangkan ruang vektor \(R^3\).

Contoh 3: Rentang

Tentukan apakah \(v_1 = (1, 1, 2), v_2 = (1, 0, 1)\) dan \(v_3 = (2, 1, 3)\) merentang \(R^3\).

Pembahasan:

Kita harus menentukan apakah sebarang vektor \(b = (b_1, b_2, b_3)\) pada \(R^3\) dapat dinyatakan sebagai kombinasi linear

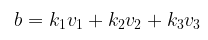
dari vektor-vektor \(v_1, v_2\), dan \(v_3\). Dengan menyatakan persamaan ini dalam komponen-komponen maka akan memberikan

Penyamaan komponen-komponen yang bersesuaian memberikan

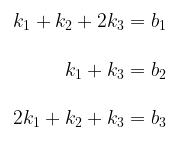
Jadi soal tersebut direduksi untuk menentukan apakah sistem ini konsisten atau tidak bagi semua nilai \(b_1, b_2\), dan \(b_3\). Sistem persamaan ini akan konsisten untuk semua nilai \(b_1, b_2\), dan \(b_3\) jika dan hanya jika matriks koefisien-koefisien

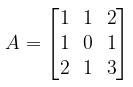
dapat dibalik. Tetapi \(\det(A) = 0\), sehingga \(A\) tidak dapat dibalik, dan sebagai konsekuensinya, maka \(v_1, v_2\), dan \(v_3\) tidak merentang \(R^3\).

Contoh 4: Rentang

Tentukan apakah \(v_1 = (1, 1, 1, -3), v_2 = (1, 1, -2, 0)\), dan \(v_3 = (1, -1, 0, 0)\) merentangkan vektor \(u = (2, -1, 2, -3)\) pada ruang vektor \(R^4\)?

Pembahasan:

Kita harus menentukan apakah vektor \(u = (2, -1, 2, -3)\) di \(R^4\) dapat dinyatakan sebagai kombinasi linier dari vektor \(v_1, v_2\), dan \(v_3\) dalam bentuk persamaan:

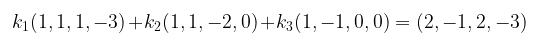
Penyamaan komponen-komponen yang bersesuaian memberikan

Dari persamaan (4) didapat \(k_1 = 1\). Dengan melakukan substitusi balik ke persamaan (3), (2), dan (1) akan diperoleh solusi untuk sistem persamaan tersebut, yakni: \(k_1 = 1, k_2 = -0,5, k_3 = 1,5\). Dengan demikian ,dapat disimpulkan bahwa \(v_1, v_2\), dan \(v_3\) merentangkan vektor \(u = (2, -1, 2, -3)\) pada ruang vektor \(R^4\).