www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Nilai Eigen & Vektor Eigen › Nilai Eigen dan Vektor Eigen: Materi, Contoh Soal dan Pembahasan
Nilai Eigen dan Vektor Eigen: Materi, Contoh Soal dan Pembahasan
Jika \(A\) adalah matriks n x n, maka vektor taknol \(x\) dinamakan vektor eigen (eigenvector) dari \(A\) jika \(Ax\) adalah kelipatan skalar dari \(x\); yakni \(Ax=λx\). Skalar \(λ\) dinamakan nilai eigen (eigenvalue) dari \(A\) dan \(x\) dikatakan vektor eigen yang bersesuaian dengan \(λ\).
Konsep mengenai nilai eigen dan vektor eigen ini memiliki aplikasi dalam berbagai bidang ilmu seperti statistika, ekonomi, komputer dan ilmu lainnya. Kita nyatakan definisi nilai eigen dan vektor eigen sebagai berikut.
Definisi: Nilai Eigen dan Vektor Eigen
Jika A adalah matriks n x n, maka vektor taknol \(x\) di dalam \(R^n\) dinamakan vektor eigen (eigenvector) dari A jika \(Ax\) adalah kelipatan skalar dari \(x\); yakni, \[Ax=λx\] untuk suatu skalar \(λ\). Skalar \(λ\) dinamakan nilai eigen (eigenvalue) dari A dan \(x\) dikatakan vektor eigen yang bersesuaian dengan \(λ\).
Adapun syarat bahwa eigen vektor adalah taknol diberlakukan untuk menghindari kasus yang tidak penting seperti \(A 0 = λ 0\), yang mana berlaku untuk setiap \(A\) dan \(λ\).
Contoh 1: Eigen Vektor dari Matriks 2 x 2
Vektor \( x= \left[ {\begin{array}{cc} 1 \\ 2 \\ \end{array} } \right] \) adalah vektor eigen dari

yang bersesuaian dengan nilai eigen \(λ=3\) karena

Secara geometris, perkalian terhadap A telah merentangkan vektor \(x\) dengan faktor 3 (Perhatikan Gambar 1).

Gambar 1
Tujuan kita selanjutnya adalah mencari prosedur umum untuk mencari nilai eigen dan vektor eigen dari matriks \(A\) berukuran \(n×n\). Kita akan mulai dengan masalah pencarian nilai eigen dari \(A\). Pertama, perhatikanlah bahwa persamaan \(A x = λ x\) bisa dituliskan kembali sebagai \(Ax= λIx\), atau secara ekivalen, sebagai \[ (λI-A)x = 0 \]
Supaya \(λ\) menjadi nilai eigen dari \(A\), maka \(x\) harus merupakan vektor tak nol. Sistem persamaan linear di atas akan mempunyai penyelesaian jika dan hanya jika koefisien matriks \((λI-A)\) mempunyai determinan nol. Oleh karena itu, kita bisa merumuskannya menjadi sebuah teorema berikut.
Teorema:
Jika \(A\) adalah sebuah matriks berukuran \(n×n\), maka \(λ\) adalah nilai eigen dari \(A\) jika dan hanya jika ia memenuhi persamaan
| \[det(λI-A) = 0\] | (1) |
Persamaan tersebut disebut persamaan karakteristik dari \(A\).
Contoh 2: Mencari Nilai Eigen
Dalam Contoh 1, kita telah mengetahui bahwa \(λ=3\) merupakan nilai eigen dari matriks

Namun, kita tidak menjelaskan bagaimana menemukannya. Sekarang kita akan menggunakan persamaan karakteristik untuk mencari semua nilai eigen dari matriks ini.
Dari persamaan (1) bahwa nilai eigen dari \(A\) merupakan solusi dari persamaan \(det(λI-A) =0 \), yang mana bisa dituliskan sebagai

Sehingga, kita peroleh:
| \[(λ-3)(λ+1)=0\] | (2) |
Ini menunjukkan bahwa nilai eigen dari \(A\) adalah \(λ=3\) dan \(λ=-1\). Oleh karena itu, selain nilai eigen \(λ=3\) yang ada pada Contoh 1, kita juga menemukan nilai eigen yang kedua yaitu \(λ=-1\).
Contoh 3: Tidak Ada Nilai Eigen
Carilah nilai-nilai eigen dari matriks
\[ A = \left[ {\begin{array}{rr} -2 & -1 \\ 5 & 2\\ \end{array} } \right] \]
Pembahasan:
Dengan melakukan cara yang sama seperti pada Contoh 2, maka
\[ A = \left| {\begin{array}{cc} λ+2 & 1 \\ -5 & λ-2\\ \end{array} } \right| = λ^2+1 \]
sehingga nilai-nilai eigen dari \(A\) harus memenuhi persamaan kuadratik \(λ^2+1=0\). Karena solusi dari persamaan ini hanyalah bilangan-bilangan imajiner \(λ=i\) dan \(λ=-i\), dan karena kita menganggap bahwa semua skalar kita adalah bilangan riil, maka \(A\) tidak mempunyai nilai eigen.
Ketika determinan \(det(λI-A)\) dalam persamaan (1) diperluas, maka persamaan karakteristik dari \(A\) akan berbentuk
| \[λ^n+c_1λ^{n-1}+\dotsc+c_n=0 \] | (3) |
di mana ruas kiri persamaan ini merupakan sebuah polinomial dengan derajat \(n\), yang mana koefisien dari \(λ^n\) adalah 1. Bentuk polinomial
| \[p(λ)=λ^n+c_1λ^{n-1}+\dotsc+c_n \] | (4) |
disebut polinomial karakteristik dari \(A\). Sebagai contoh, pada persamaan (2), polinomial karakteristik dari matriks berukuran \(2×2\) pada Contoh 2 adalah

yang merupakan polinomial dengan derajat 2.
Karena polinomial derajat \(n\) memiliki setidaknya \(n\) akar yang berbeda, maka dari persamaan (3), persamaan karakteristik dari matriks \(A\) berukuran \(n×n\) memiliki setidaknya \(n\) solusi yang berbeda dan akibatnya matriks tersebut memiliki setidaknya \(n\) nilai eigen yang berbeda.
Contoh 4: Nilai Eigen dari Matriks Berukuran \(3×3\)
Carilah nilai-nilai eigen dari
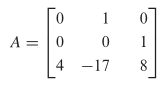
Pembahasan:
Polinomial karakteristik dari \(A\) yaitu

Oleh karena itu, nilai-nilai eigen dari \(A\) harus memenuhi persamaan kubik berikut
| \[λ^3-8λ^2+17λ-4=0 \] | (5) |
Persamaan (5) dapat dituliskan menjadi
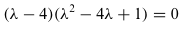
Sehingga nilai-nilai eigen dari \(A\) adalah
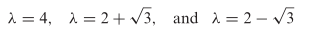
Teorema berikut memberikan beberapa cara alternatif untuk menjelaskan nilai eigen.
Teorema:
Jika \(A\) adalah matriks berukuran \(n×n\), maka pernyataan berikut adalah ekivalen.
- \(λ\) adalah sebuah nilai eigen dari \(A\)
- \(λ\) adalah sebuah solusi dari persamaan karakteristik \(det(λI-A)=0\).
- Sistem persamaan \((λI-A)x=0\) mempunyai solusi taktrivial.
- Terdapat sebuah vektor \(x\) yang taknol sehingga \(Ax= λx\)
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
It takes 20 years to build a reputation and five minutes to ruin it. If you think about that, you’ll do things differently.
