www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Matriks › Operasi Matriks
Operasi Matriks
Sama halnya dengan bilangan, dua matriks atau lebih juga bisa ditambahkan, dikurangkan, dan dikalikan untuk menghasilkan suatu matriks baru.
Sama halnya dengan bilangan yang bisa ditambahkan, dikurangkan, dan dikalikan untuk menghasilkan bilangan yang baru, demikian pula dengan matriks yang mana juga bisa ditambahkan, dikurangkan, dan dikalikan untuk menghasilkan suatu matriks baru.
Kita akan memulai operasi penghitungan sederhana dari matriks yang meliputi kesamaan dua matriks, operasi penjumlahan dan pengurangan matriks serta perkalian matriks.
Kesamaan Dua Matriks
Dua matriks dikatakan sama jika kedua matriks tersebut mempunyai ukuran yang sama dan entri-entri yang bersesuaian dalam kedua matriks tersebut juga sama. Dengan demikian, dua buah matriks A dan B dikatakan sama jika dan hanya jika \(A_{mn}=A_{nm}\) untuk setiap m dan n.
Sebagai contoh, diberikan dua matriks yakni
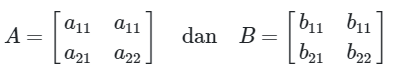
Jika matriks A = B, maka \(a_{11} = b_{11}, \ a_{12} = b_{12}, \ a_{21} = b_{21}\) dan \(a_{22} = b_{22}\).
Contoh 1: Kesamaan Dua Matriks
Tinjaulah matriks-matriks berikut ini.

Matriks A tidak sama dengan matriks C atau A ≠ C, karena A dan C mempunyai ukuran yang tidak sama. Begitu juga dengan matriks B ≠ C karena mempunyai ukuran yang berbeda. Selain itu, matriks A tidak sama dengan matriks B atau A ≠ B karena entri/elemen yang bersesuaian dari kedua matriks tidak semuanya sama.
Contoh 2: Kesamaan Dua Matriks
Tentukan x dan y jika diketahui A = B.

Penyelesaian:
Karena A = B, maka x - 2y = -6 dan 2x + y = 8. Untuk mencari nilai x dan y, kita bisa menggunakan penyelesaian sistem persamaan linear dua variabel (SPLDV) yang telah dipelajari pada pelajaran matematika dasar di sekolah menengah. Dari hasil perhitungan diperoleh nilai x dan y yang sesuai untuk matriks A di atas adalah x = 2 dan y = 4.
Penjumlahan dan Pengurangan Matriks
Jika A dan B adalah sebarang dua matriks yang ukurannya sama, maka jumlah A + B adalah matriks baru yang diperoleh dengan menambahkan secara bersama-sama entri-entri yang bersesuain dalam kedua matriks tersebut.
Begitu juga dengan pengurangan A – B adalah matriks baru yang diperoleh dengan melakukan pengurangan secara bersama-sama entri-entri yang bersesuaian dalam kedua matriks tersebut. Hal yang perlu menjadi perhatian adalah bahwa matriks-matriks yang ukurannya berbeda tidak dapat ditambahkan atau dikurangkan.
Sebagai contoh, misalkan diketahui matriks berikut.

Dengan demikian,

Contoh 3: Penjumlahan dan Pengurangan Matriks
Tinjaulah matriks-matriks berikut ini.

Hitunglah A + B dan A - B!
Penyelesaian:
Penjumlahan matriks A dan B atau A + B adalah:
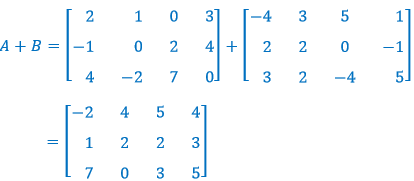
dan, pengurangan matriks A dan B atau A - B adalah:
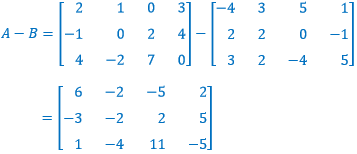
Untuk A + C atau A - C dan B + C atau B - C tidak bisa dihitung karena mempunyai ukuran matriks yang berbeda.
Perkalian Skalar dengan Matriks
Jika A adalah suatu matriks dan c adalah suatu skalar, maka hasil kali (product) cA adalah matriks baru yang diperoleh dengan mengalikan masing-masing entri dari A dengan c.
Contoh 4: Perkalian Skalar dengan Matriks
Misalkan diketahui matriks-matriks sebagai berikut.

Dengan demikian,

Perkalian Matriks
Jika A adalah matriks m x r dan B adalah matriks r x n, maka hasil kali AB adalah matriks m x n di mana untuk mencari entri dalam baris \(i\) dan kolom \(j\) dari AB, pilihlah baris \(i\) dari matriks A dan kolom \(j\) dari matriks B. Kalikan entri-entri yang bersesuaian dari baris dan kolom tersebut secara bersama-sama dan kemudian tambahkanlah hasil kali yang dihasilkan. Untuk lebih jelasnya perhatikanlah contoh berikut.
Contoh 5: Perkalian Matriks
Tinjaulah matriks-matriks berikut.

Karena A adalah matriks \(2 × 3\) dan B adalah matriks \(3 × 4\), maka hasilkali AB adalah matriks \(2 × 4\). Untuk menentukan, misalnya, entri dalam baris 2 dan kolom 3 dari AB, kita dapat memilih baris 2 dari A dan kolom 3 dari B. Maka, seperti yang dilukiskan di bawah, kita dapat mengalikan entri-entri yang bersesuaian bersama-sama dan menambah hasil kali ini.

Entri dalam baris 1 dan kolom 4 dari AB dihitung sebagai berikut.

Penghitungan-penghitungan untuk hasilkali selebihnya dan matriks AB diberikan di bawah ini.
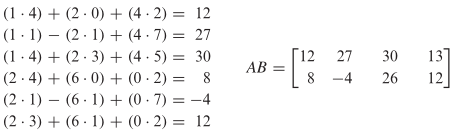
Hal penting yang perlu diingat adalah bahwa definisi perkalian matriks mengharuskan banyaknya kolom dari faktor pertama A harus sama seperti banyaknya baris dari faktor kedua B supaya membentuk hasilkali AB. Jika kondisi ini tidak dipenuhi, maka hasil kali tersebut tidak dapat didefinisikan.
Sebuah cara mudah untuk menentukan apakah hasil kali dua matriks dapat didefinisikan adalah dengan menulis ukuran faktor pertama, dan ke sebelah kanannya, kita menuliskan ukuran faktor kedua, seperti dalam ilustrasi berikut.

Jika bilangan-bilangan yang di sebelah dalam (inside) adalah sama, maka hasil kalinya dapat didefinisikan. Bilangan-bilangan yang di sebelah luar (outside) akan memberikan ukuran hasil kali tersebut. Sebaliknya, jika bilangan-bilangan yang di sebelah dalam (inside) adalah tidak sama, maka hasil kali kedua matriks tidak dapat didefinisikan.
Contoh 6: Perkalian Matriks
Misalkan A adalah matriks 3 x 4, B adalah matriks 4 x 7, dan C adalah matriks 7 x 3. Maka hasilkali AB didefinisikan sebagai matriks 3 x 7; CA didefinisikan sebagai matriks 7 x 4; BC didefinisikan sebagai matriks 4 x 3. Hasilkali AC, CB, dan BA semuanya tidak dapat didefinisikan.
Secara umum, jika \(A=[a_{ij}]\) adalah matriks m x r dan \(B=[b_{ij}]\) adalah matriks r x n, maka seperti diilustrasikan oleh daerah yang diwarnai biru pada tampilan berikut,

entri-entri \((AB)_{ij}\) pada baris \(i\) dan kolom \(j\) dari AB diberikan oleh

Formula ini disebut aturan baris-kolom (row-column rule) untuk perkalian matriks.
Transpos Matriks
Jika A adalah sebarang matriks m x n, maka transpos A dinyatakan oleh \(A^T\) dan didefinisikan dengan matriks n x m yang kolom pertamanya adalah baris pertama dari A, kolom keduanya adalah baris kedua dari A, demikian juga dengan kolom ketiga adalah baris ketiga dari A, dan seterusnya.
Berikut ini diberikan beberapa contoh matriks beserta transposnya.

Perhatikanlah bahwa tidak hanya kolom-kolom \(A^T\) yang merupakan baris dari A, namun baris \(A^T\) juga merupakan kolom dari A. Oleh karena itu, entri pada baris \(i\) dan kolom \(j\) matriks \(A^T\) adalah entri pada baris \(j\) dan kolom \(i\) dari matriks A; yaitu
\[ (A^T )_{ij}=(A)_{ji} \]
(Perhatikanlah kebalikan dari subscript-nya)
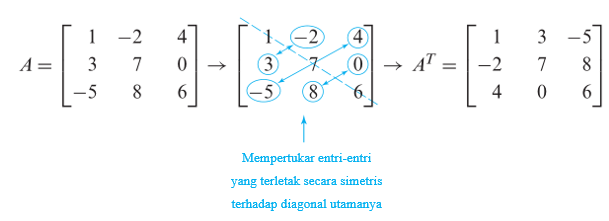
Dalam kasus khusus di mana A adalah matriks persegi, transpos A bisa diperoleh dengan mempertukarkan entri yang terletak secara simetris terhadap diagonal utamanya. Pada contoh matriks berikut kita melihat bahwa \(A^T\) juga bisa diperoleh dengan “mencerminkan” A terhadap diagonal utamanya.
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Jumping from failure to failure with undiminished enthusiasm is the big secret to success.
