www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Vektor & Ruang Vektor › Kombinasi Linier Vektor: Materi, Contoh Soal dan Pembahasan
Kombinasi Linier Vektor: Materi, Contoh Soal dan Pembahasan
Salah satu pembahasan penting berkaitan dengan ruang vektor adalah kombinasi linear vektor. Setelah memahami kombinasi linear vektor, kita dapat memberikan definisi terhadap apa yang disebut himpunan bebas linear dan bergantung linear, serta himpunan yang membangun ruang vektor.
Kita definisikan kombinasi linear vektor berikut ini.
Definisi:
Sebuah vektor \(w\) dinamakan kombinasi linear dari vektor-vektor \(v_1, v_2, ..., v_r\) jika vektor tersebut dapat dinyatakan dalam bentuk
di mana \(k_1, k_2,...,k_r\) adalah skalar.
Contoh 1:
Periksalah apakah \( w = (3,5) \) merupakan kombinasi linear dari \( u = (1,1) \) dan \( v = (1,2) \).
Pembahasan:
Untuk menentukan apakah \(w\) merupakan kombinasi linear dari \(u\) dan \(v\), kita perlu memeriksa apakah terdapat skalar-skalar \(k_1\) dan \(k_2\) yang memenuhi \( w = k_1 u + k_2 v \), yaitu
Berdasarkan kesamaan dua vektor, diperoleh sistem persamaan linear berikut.
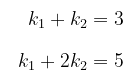
Solusi dari sistem persamaan tersebut di atas adalah \( k_1 = 1 \) dan \( k_2 = 2 \). Jadi, karena terdapat skalar-skalar \( k_1 \) dan \( k_2 \) yang memenuhi \( w = k_1 u + k_2 v \), maka \(w\) merupakan kombinasi linear dari \( u \) dan \( v \).
Contoh 2:
Periksalah apakah \( w = (5,10) \) merupakan kombinasi linear dari \( u = (1,2) \) dan \( v = (2,4) \).
Pembahasan:
Untuk menentukan apakah \(w\) merupakan kombinasi linear dari \(u\) dan \(v\), kita perlu memeriksa apakah terdapat skalar-skalar \(k_1\) dan \(k_2\) yang memenuhi \( w = k_1 u + k_2 v \), yaitu
Berdasarkan kesamaan dua vektor, diperoleh sistem persamaan linear berikut.
Matriks yang diperbesar dari sistem persamaan di atas adalah
dengan bentuk eselon baris
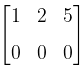
Solusi dari sistem persamaan di atas dapat dinyatakan dalam persamaan parametrik, yakni
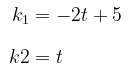
Jadi, karena terdapat skalar-skalar \( k_1 \) dan \( k_2 \) yang memenuhi \( w = k_1 u + k_2 v \), maka \(w\) merupakan kombinasi linear dari \( u \) dan \( v \). Lebih lanjut, ada tak berhingga cara menuliskan \( w \) sebagai kombinasi linear dari \( u \) dan \( v \).
Contoh 3:
Tinjaulah vektor-vektor \(u = (1, 2, -1)\) dan \(v = (6, 4, 2)\) di R3. Perlihatkan bahwa \(w = (9, 2, 7)\) adalah kombinasi linear \(u\) dan \(v\) serta bahwa \(w'=(4, -1, 8)\) bukanlah kombinasi linear \(u\) dan \(v\).
Penyelesaian:
Supaya \(w\) merupakan kombinasi linear \(u\) dan \(v\), harus ada skalar \(k_1\) dan \(k_2\) sehingga \( w=k_1 u + k_2 v \); yakni
Penyamaan komponen-komponen yang bersesuaian memberikan
Dengan memecahkan sistem ini akan menghasilkan \( k_1 = -3\) dan \( k_2 = 2 \) sehingga
Demikian juga, supaya \(w'\) merupakan kombinasi linear \(u\) dan \(v\), harus ada skalar \(k_1\) dan \(k_2\) sehingga \( w'=k_1 u + k_2 v \); yaitu
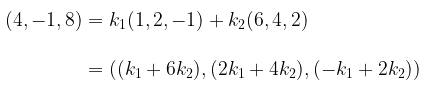
Dengan menyamakan komponen yang bersesuaian memberikan
Sistem persamaan-persamaan ini tidak konsisten, sehingga tidak ada skalar-skalar seperti itu. Sebagai konsekuensinya, maka \(w'\) bukanlah kombinasi linear \(u\) dan \(v\).
Contoh 4:
Periksalah apakah \( w = (3,5,7) \) merupakan kombinasi linear dari vektor-vektor \( u_1 = (1,1,2)\), \(u_2 = (1,0,1)\), dan \( u_3 = (2,1,3) \).
Pembahasan:
Kita perlu memeriksa apakah terdapat skalar-skalar \( k_1, k_2, \) dan \( k_3 \) yang memenuhi
Berdasarkan kesamaan dua vektor, diperoleh sistem persamaan linear
Matriks yang diperbesar dari sistem persamaan di atas adalah
Dengan serangkaian operasi baris elementer, diperoleh bentuk eselon baris dari matriks di atas, yaitu
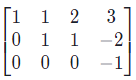
Persamaan yang bersesuaian dengan baris ketiga adalah \( 0 = -1 \) yang jelas bernilai salah. Akibatnya, 
tidak mempunyai solusi. Dengan demikian, \( w \) bukan kombinasi linear dari \( u_1, u_2 \) dan \( u_3 \).
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Too many of us are not living our dreams because we are living our fears.