www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Aljabar Linear   »   Vektor & Ruang Vektor   ›  Definisi, Notasi, dan Operasi Vektor: Materi, Contoh Soal dan Pembahasan
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Vektor

Definisi, Notasi, dan Operasi Vektor: Materi, Contoh Soal dan Pembahasan

Vektor dapat dinyatakan secara geometris dengan segmen-segmen garis yang mempunyai arah atau panah-panah di ruang-2 atau 3 dimensi.

Flag Counter

Dalam matematika, vektor adalah objek geometri yang memiliki besar dan arah. Contoh dari vektor misalnya adalah gaya, kecepatan, perpindahan dan lainnya. Vektor dapat dinyatakan secara geometris dengan segmen-segmen garis yang mempunyai arah atau panah-panah di ruang-2 atau 3 dimensi.

Arah panah menentukan arah vektor dan panjang panah menyatakan besar vektor. Ekor panah dinamakan titik awal (initial point) dari vektor, dan ujung panah dinamakan titik terminal (terminal point).

Gambar

Gambar 1.

Kita dapat menyatakan vektor dengan huruf kecil tebal misalnya: a, k, v, w, dan x atau dengan memberikan tanda panah di atas huruf, misalnya: \( \vec{u}, \overrightarrow{AB} \). Ketika membahas vektor, kita akan menyatakan bilangan sebagai skalar. Semua skalar merupakan bilangan riil dan akan dinyatakan oleh huruf kecil biasa misalnya, a, k, v, w dan x.

Sebagai contoh vektor, perhatikanlah Gambar 2. Titik awal (initial point) dari vektor \(v\) adalah \(A\) dan titik terminalnya (terminal point) adalah titik \(B\), sehingga kita bisa menuliskan: \[ \textbf{v} = \overrightarrow{AB} \]

notasi vektor

Gambar 2.

Vektor-vektor yang mempunyai panjang dan arah yang sama, seperti vektor-vektor pada Gambar 3, dinamakan vektor yang ekivalen. Jika \(v\) dan \(w\) ekivalen maka kita dapat menuliskan: \[v=w\]

vektor ekivalen

Gambar 3.

Operasi Vektor

Setelah memahami definisi vektor di atas, sekarang kita akan membahas operasi-operasi pada vektor. Operasi vektor meliputi penjumlahan dan pengurangan vektor, perkalian vektor dengan skalar, perkalian titik vektor, dan perkalian silang vektor.

Untuk operasi penjumlahan dua vektor, terdapat dua macam cara penjumlahan yang bisa digunakan, yaitu: cara segitiga dan cara jajar genjang.

Definisi: Aturan Jajar Genjang untuk Penjumlahan Vektor

Jika \(v\) dan \(w\) adalah vektor dalam ruang 2 atau 3 dimensi yang diposisikan sehingga titik awalnya berimpit, maka kedua vektor membentuk sisi yang berdekatan dari jajar genjang, dan jumlah vektor \(v + w\) adalah vektor yang diwakili oleh panah dari titik awal \(v\) dan \(w\) ke titik berlawanan dari jajar genjang (Perhatikan Gambar 4.a).

Definisi: Aturan Segitiga untuk Penjumlahan Vektor

Jika \(v\) dan \(w\) adalah sebarang dua vektor, maka jumlah \(v+w\) adalah vektor yang ditentukan dengan menempatkan vektor \(w\) sehingga titik awalnya berimpit dengan titik terminal \(v\). Vektor \(v+w\) dinyatakan oleh panah dari titik awal \(v\) terhadap titik terminal \(w\) (Perhatikan Gambar 4.b).

Ilustrasi Penjumlahan Vektor

Gambar 4.

Dalam Gambar 4c kita membentuk dua jumlah vektor, yakni \(v+w\) (panah biru) dan w+v (panah putih) di mana \[v+w=w+v\]

dan terlihat bahwa jumlah vektor tersebut berimpit dengan diagonal jajaran genjang yang ditentukan oleh \(v\) dan \(w\) bila vektor-vektor ini dilokasikan sehingga vektor-vektor tersebut mempunyai titik awal yang sama.

Jika \(v\) adalah sebarang vektor taknol, maka \(–v\) adalah negatif, yang didefinisikan sebagai vektor yang mempunyai besaran sama seperti \(v\), tetapi mempunyai arah yang berlawanan dengan \(v\) (Gambar 5.a).

vektor negatif

Gambar 5.

Definisi: Pengurangan Vektor

Jika \(v\) dan \(w\) adalah sebarang dua vektor, pengurangan \(v\) dari \(w\) didefinisikan oleh \[w-v=w+(-v)\] Perhatikan Gambar 5.b dan 5.c untuk ilustrasi pengurangan vektor.

Untuk mendapatkan selisih \(w-v\) tanpa menggambarkan \(–v\), maka tempatkanlah \(v\) dan \(w\) sehingga titik awalnya berimpit; vektor dari titik terminal \(w\) ke titik terminal \(v\) adalah vektor \(w-v\) (Gambar 5.c).

Definisi: Perkalian Skalar

Jika \(v\) adalah vektor taknol dan \(k\) bilangan riil taknol (skalar), maka hasil kali \(kv\) didefinisikan sebagai vektor yang panjangnya \(|k|\) kali panjang \(v\) dan yang arahnya sama seperti arah \(v\) jika \(k > 0\) dan berlawanan dengan arah \(v\) jika \(k < 0\). Kita definisikan \(kv=0\) jika \(k = 0\) atau \(v = 0\).

Gambar 6 melukiskan hubungan di antara vektor \(v\) dan vektor-vektor \(\frac{1}{2}v, (-1)v, 2v\), dan \((-3)v\).

ilustrasi perkalian skalar vektor

Gambar 6.

Perhatikan bahwa vektor \((-1)v\) mempunyai panjang yang sama seperti \(v\) tetapi mempunyai arah yang berlawanan. Jadi \((-1)v\) tak lain adalah negatif \(v\); yakni, \[(-1)v=-v\]

Vektor dalam Sistem Koordinat

Jika sebuah vektor \(v\) dalam ruang 2 atau ruang 3 dimensi diposisikan sehingga titik awalnya berada di titik asal sistem koordinat siku-sku, maka vektor tersebut ditentukan oleh koordinat titik terminalnya (Gambar 7). Kita sebut koordinat tersebut sebagai komponen-komponen vektor \(v\) yang relatif terhadap sistem koordinat.

Kita akan menuliskan \(v=(v_1,v_2)\) untuk menotasikan sebuah vektor \(v\) dalam ruang 2 dimensi dengan komponen-komponennya adalah \((v_1,v_2)\) dan \(v=(v_1,v_2,v_3)\) untuk menotasikan sebuah vektor \(v\) dalam ruang 3 dimensi dengan komponen-komponennya yaitu \((v_1,v_2,v_3)\).

vektor dalam sistem koordinat

Gambar 7.

Vektor dengan komponen yang sama harus mempunyai panjang dan arah yang sama, dan sebagai konsekuensinya vektor-vektor tersebut ekivalen. Sebagai contoh, dua vektor berikut

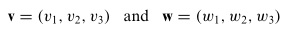
vektor ekivalen

dalam ruang 3 dimensi adalah ekivalen jika dan hanya jika

vektor ekivalen

Operasi penambahan vektor dan operasi perkalian vektor dengan skalar dalam komponen-komponen vektor diilustrasikan pada Gambar 8. Seperti yang terlihat pada Gambar 8, jika \(v = (v_1, v_2)\) dan \(w=(w_1,w_2) \) maka \[ v+w=(v_1+w_2, v_2+w_2)\]

\[kv= (kv_1, kv_2) \]

operasi vektor dalam sistem koordinat

Gambar 8.

Contoh 1:

Misalkan diketahui vektor \(v=(1,-2)\) dan \(w=(7,6)\). Tentukanlah vektor \( v+w, \ v-w \) dan \(4v\).

Pembahasan:

Sesuai dengan penjelasan sebelumnya, maka kita peroleh:

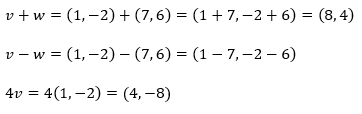
contoh operasi vektor
Contoh 2:

Jika \(v=(1,-3,2)\) dan \(w=(4,2,1)\), maka kita peroleh berikut:

contoh operasi vektor
Contoh 3:

Diketahui vektor \( \overrightarrow{AB} = (-2, 1, 4) \). Jika vektor posisi titik \(B = (1,-2,1) \), maka vektor posisi titik \(A\) adalah…

  1. \( (3,-3,-3) \)
  2. \( (1,-2,1) \)
  3. \( (-3,-2,3) \)
  4. \( (1,-3,0) \)
  5. \( (4,-2,-3) \)
Pembahasan »

Ingat bahwa komponen vektor \( \overrightarrow{AB} \) merupakan hasil pengurangan antara vektor posisi titik B dan titik A, sehingga kita peroleh berikut:

\begin{aligned} \overrightarrow{AB} &= B - A \\[8pt] (-2,1,4) &= (1,-2,1)-A \\[8pt] A &= (1,-2,1)-(-2,1,4) \\[8pt] &= (1-(-2), \ -2-1, \ 1-4) \\[8pt] &= (3,-3,-3) \end{aligned}

Jawaban A.

Contoh 4:

Diketahui dua buah vektor posisi yaitu \( \vec{p} = \hat{i}-2\hat{j}-\hat{k} \) dan \( \vec{q} = 2\hat{i}-3\hat{j}+\hat{k} \). Vektor \( \overrightarrow{PQ} = \cdots \)

  1. \( \hat{i}-2\hat{j}-2\hat{k} \)
  2. \( \hat{i}-\hat{j}+2\hat{k} \)
  3. \( 3\hat{i}-\hat{j}-2\hat{k} \)
  4. \( \hat{i}+\hat{j}+2\hat{k} \)
  5. \( \hat{i}-2\hat{j}+\hat{k} \)
Pembahasan »

Vektor \( \overrightarrow{PQ}\) merupakan hasil pengurangan antara vektor posisi di titik \( P \) dan vektor posisi di titik \(Q\). Dengan demikian, kita peroleh berikut:

\begin{aligned} \overrightarrow{PQ} &= q - p \\[8pt] &= (2\hat{i}-3\hat{j}+\hat{k})-(\hat{i}-2\hat{j}-\hat{k}) \\[8pt] &= (2-1)\hat{i}+(-3-(-2))\hat{j}+(1-(-1))\hat{k} \\[8pt] &= \hat{i}-\hat{j}+2\hat{k} \end{aligned}

Jawaban B.

Contoh 5:

Diketahui dua buah vektor yakni \( \vec{a} = (x+3) \hat{i}-5\hat{j}+4\hat{k} \) dan \( \vec{b} = 2\hat{i}+y\hat{j}-6\hat{k} \). Jika hasil penjumlahan kedua vektor tersebut menghasilkan \( \vec{a}+\vec{b} = (10,-4,-2) \) maka nilai \( x+y = \cdots \)

  1. \( 9 \)
  2. \( 8 \)
  3. \( 7 \)
  4. \( 6 \)
  5. \( 5 \)
Pembahasan »

Nilai \(x+y\) dapat dicari sebagai berikut:

\begin{aligned} \vec{a}+\vec{b} &= \begin{pmatrix} x+3 \\ -5 \\ 4 \end{pmatrix} + \begin{pmatrix} 2 \\ y \\ -6 \end{pmatrix} \\[8pt] \begin{pmatrix} 10 \\ -4 \\ -2 \end{pmatrix} &= \begin{pmatrix} x+5 \\ y-5 \\ -2 \end{pmatrix} \\[8pt] x+5 &= 10 \Leftrightarrow x = 10-5=5 \\[8pt] y-5 &= -4 \Leftrightarrow y = -4+5=1 \\[8pt] x+y &= 5+1 = 6 \end{aligned}

Jawaban D.

Contoh 6:

Jika \( \vec{a} = (-1,3,2), \ \vec{b} = (4,-3,-2) \) dan \( 2\vec{a}+\vec{x}-3\vec{b} = (-11,5,12) \), maka \( \vec{x} = \cdots \)

  1. \( (3, -10, 2) \)
  2. \( (2, -10, 3) \)
  3. \( (-10,3,2) \)
  4. \( (10,2,3) \)
  5. \( (3,2,10) \)
Pembahasan »

Vektor \( \vec{x} \) dapat dicari sebagai berikut:

\begin{aligned} 2\vec{a}+\vec{x}-3\vec{b} &= \begin{pmatrix} -11 \\ 5 \\ 12 \end{pmatrix} \\[8pt] 2 \begin{pmatrix} -1 \\ 3 \\ 2 \end{pmatrix} + \vec{x}-3 \begin{pmatrix} 4 \\ -3 \\ -2 \end{pmatrix} &= \begin{pmatrix} -11 \\ 5 \\ 12 \end{pmatrix} \\[8pt] \begin{pmatrix} -2 \\ 6 \\ 4 \end{pmatrix}+\vec{x}-\begin{pmatrix} 12 \\ -9 \\ -6 \end{pmatrix} &= \begin{pmatrix} -11 \\ 5 \\ 12 \end{pmatrix} \\[8pt] \vec{x} &= \begin{pmatrix} -11 \\ 5 \\ 12 \end{pmatrix}-\begin{pmatrix} -2 \\ 6 \\ 4 \end{pmatrix}+\begin{pmatrix} 12 \\ -9 \\ -6 \end{pmatrix} \\[8pt] &= \begin{pmatrix} -11+2+12 \\ 5-6-9 \\ 12-4-6 \end{pmatrix} = \begin{pmatrix} 3 \\ -10 \\ 2 \end{pmatrix} \end{aligned}

Jawaban A.

Contoh 7:

Berapakah nilai \( \alpha \) dan \( \beta \) yang memenuhi \( \alpha (3,5) + \beta(4,7) = (6,3) \).

  1. 30 dan 21
  2. -21 dan 30
  3. -30 dan -21
  4. 30 dan -21
  5. 21 dan -30
Pembahasan »

Nilai \( \alpha \) dan \( \beta \) dapat diperoleh sebagai berikut:

\begin{aligned} \alpha (3,5) + \beta(4,7) &= (6,3) \\[8pt] (3\alpha+5\alpha)+(4\beta+7\beta) &= (6,3) \\[8pt] (3\alpha + 4\beta, 5 \alpha + 7 \beta) &= (6,3) \\[8pt] 3\alpha + 4\beta &= 6 \\[8pt] 5 \alpha + 7 \beta &= 3 \\[8pt] \alpha = 30 \ \text{dan} \ \beta &= -21 \end{aligned}

Jawaban D.

Contoh 8:

Agar kedua vektor \( \vec{a} = (x,4,7) \) dan \( \vec{b} = (6,y,14) \) adalah segaris, maka nilai \(x-y\) harus sama dengan….

  1. 5
  2. 6
  3. -5
  4. -6
  5. -7
Pembahasan »

Agar vektor \( \vec{a} \) kolinear atau segaris dengan vektor \(\vec{b}\), maka

\begin{aligned} \vec{a} &= k \cdot \vec{b} \\[8pt] (x,4,7) &= k(6,y,14) \\[8pt] 7 &= 14k \Leftrightarrow k = \frac{1}{2} \\[8pt] x &= 6k \Leftrightarrow x = 6 \cdot \frac{1}{2} = 3 \\[8pt] 4 &= ky \Leftrightarrow 4 = \frac{1}{2} y \Rightarrow y = 8 \\[8pt] x-y &= 3-8=-5 \end{aligned}

Jawaban C.

Contoh 9:

Diberikan tiga buah ektor masing-masing sebagai berikut: \( \vec{p} = \hat{i}+\hat{j}+\hat{k}, \ \vec{q}= 2\hat{i}-3\hat{j}+\hat{k} \) dan \( \vec{r}=-2\hat{j}-3\hat{k} \). Jika \( \vec{s} = 2\vec{p}-\vec{q}+3\vec{r} \), maka \( \vec{s} = \cdots \)

  1. \( \hat{i}+2\hat{j}-7\hat{k} \)
  2. \( -\hat{i}+6\hat{k} \)
  3. \( 6\hat{i}+7\hat{k} \)
  4. \( -\hat{j}-8\hat{k} \)
  5. \( \hat{j}+4\hat{k} \)
Pembahasan »

Vektor \(\vec{s}\) dapat dicari sebagai berikut:

\begin{aligned} \vec{s} &= 2\vec{p}-\vec{q}+3\vec{r} \\[8pt] &= 2 (\hat{i}+\hat{j}+\hat{k})-(2\hat{i}-3\hat{j}+\hat{k})+3(-2\hat{j}-3\hat{k}) \\[8pt] &= (2\hat{i}+2\hat{j}+2\hat{k})-(2\hat{i}-3\hat{j}+\hat{k})+(-6\hat{j}-9\hat{k}) \\[8pt] &= (2-2) \hat{i}+(2-(-3)-6) \hat{j} +(2-1-9) \hat{k} \\[8pt] &= 0 \hat{i}-\hat{j}-8\hat{k} \\[8pt] &= -\hat{j}-8\hat{k} \end{aligned}

Jawaban D.

Contoh 10:

Tiga buah titik P, Q, dan R terletak pada satu garis. Jika \(P(1,2,-1), \ Q(3,0,2)\), dan \(R(7,-4,2b+1)\), maka nilai \(b\) sama dengan…

  1. \( \frac{3}{2} \)
  2. \( \frac{5}{2} \)
  3. \( \frac{7}{2} \)
  4. \( \frac{9}{2} \)
  5. \( \frac{11}{2} \)
Pembahasan »

Karena titik P, Q, dan R dalam satu garis maka berlaku \( \overrightarrow{PQ}=k \cdot \overrightarrow{QR} \) di mana \( \overrightarrow{PQ}=Q-P \) dan \( \overrightarrow{QR}=R-Q \), sehingga kita peroleh berikut:

\begin{aligned} \overrightarrow{PQ} &= k \cdot \overrightarrow{QR} \\[8pt] Q-P &= k (R-Q) \\[8pt] \begin{pmatrix} 3 \\ 0 \\ 2 \end{pmatrix} - \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} &= k \left( \begin{pmatrix} 7 \\ -4 \\ 2b+1 \end{pmatrix} - \begin{pmatrix} 3 \\ 0 \\ 2 \end{pmatrix} \right) \\[8pt] \begin{pmatrix} 2 \\ -2 \\ 3 \end{pmatrix} &= k \begin{pmatrix} 4 \\ -4 \\ 2b-1 \end{pmatrix} \\[8pt] 2 &= 4k \Leftrightarrow k = \frac{2}{4} = \frac{1}{2} \\[8pt] 3 &= k(2b-1) \\[8pt] 3 &= \frac{1}{2}(2b-1) \\[8pt] 3 &= b-\frac{1}{2} \Leftrightarrow b = 3 + \frac{1}{2} = \frac{7}{2} \end{aligned}

Jawaban C.

Sumber:

Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan jika ada yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.

Oleh Tju Ji Long · Statistisi

Artikel Terkait
img

Perkalian titik dan perkalian silang vektor: Materi, contoh soal dan pembahasan

img

Proyeksi ortogonal vektor: Materi, contoh soal dan pembahasan

img

Contoh soal menghitung panjang vektor

img

Contoh soal menghitung sudut antara vektor


Life is not a problem to be solved, but a reality to be experienced.

Soren Kierkegaard