www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Matriks › Sifat-sifat Operasi Matriks
Sifat-sifat Operasi Matriks
Banyak aturan dasar aritmatika yang berlaku untuk bilangan riil juga berlaku untuk matriks, tetapi kita juga akan melihat beberapa aturan tersebut tidak berlaku.
Pada artikel ini kita akan membahas sifat-sifat aljabar pada operasi matriks. Kita akan melihat bahwa banyak aturan dasar aritmatika (penjumlahan, pengurangan, perkalian, dan pembagian) yang berlaku untuk bilangan riil juga berlaku untuk matriks, tetapi kita juga akan melihat bahwa beberapa aturan tersebut ternyata tidak berlaku.
Teorema berikut menyatakan sifat-sifat dari operasi matriks.
Teorema 1: Sifat-Sifat Aritmatika Matriks
Asumsikan bahwa ukuran setiap matriks yang diberikan berikut memungkinkan untuk dapat dilakukan operasi matriks. Dengan demikian, kita peroleh sifat-sifat berikut ini.

Untuk membuktikan persamaan dalam teorema di atas, kita harus menunjukkan bahwa matriks pada ruas kiri mempunyai ukuran yang sama seperti pada ruas kanan. Selain itu, entri-entri yang bersesuaian pada kedua ruas juga mesti sama. Kita akan mengambil Bagian (d) dari Teorema 1 di atas sebagai contoh.
Bukti Bagian (d):
Perhatikan bahwa pada Bagian (d), \( A(B+C)=AB+AC \). Untuk membuktikan ini, kita harus menunjukkan bahwa ruas kiri A (B + C) dan ruas kanan (AB + AC) mempunyai ukuran yang sama, begitu juga dengan entri-entri yang bersesuaian adalah sama.
Untuk bentuk A (B + C), matriks B dan C harus mempunyai ukuran yang sama, katakanlah \(m × n\), dan matriks A harus mempunyai m kolom, sehingga ukurannya harus berupa bentuk \(r×m\). Ini membuat A (B + C) dan AB + AC mempunyai ukuran yang sama.
Misalkan bahwa \(A = [a_{ij}], B = [b_{ij}]\), dan \(C = [c_{ij}]\). Kita ingin menunjukkan bahwa entri-entri yang bersesuaian dari A (B + C) dan AB + AC adalah sama; yakni:
\[\left(A(B+C) \right)_{ij} = \left(AB+AC \right)_{ij} \]
untuk semua nilai \(i\) dan \(j\). Dari definisi penjumlahan dan perkalian matriks, kita peroleh:

Dengan demikian, kita telah membuktikan sifat dalam Teorema 1 bagian (d) ini.
Terdapat tiga cara dasar untuk membuktikan bahwa dua matriks dengan ukuran yang sama adalah sama yaitu (i) membuktikan bahwa entri-entri yang bersesuaian adalah sama, (ii) membuktikan bahwa vektor baris yang bersesuaian adalah sama, atau (iii) membuktikan bahwa vektor kolom yang bersesuaian adalah sama.
Contoh 1: Perkalian matriks asosiatif
Sebagai ilustrasi hukum asosiatif untuk perkalian matriks, perhatikan tiga matriks berikut.
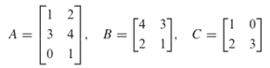
Dengan demikian,
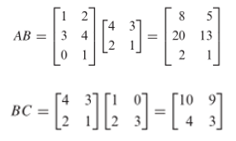
Sehingga

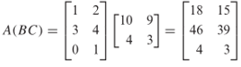
Jadi, (AB) C = A (BC), seperti yang dijamin dalam Teorema 1 (c) di atas.
Sifat dari Perkalian Matriks
Seperti telah dinyatakan di awal artikel ini bahwa banyak aturan dasar aritmatika yang berlaku untuk bilangan riil juga berlaku untuk matriks, tetapi tidak semua aturan tersebut berlaku. Dengan kata lain, jangan membiarkan Teorema 1 di atas menjebak anda untuk percaya bahwa semua hukum aritmatika riil berlaku juga untuk aritmatika matriks. Sebagai contoh, anda tahu bahwa dalam aritmatika riil selalu benar bahwa ab = ba, yang mana disebut hukum komutatif untuk perkalian. Namun, dalam aritmatika matriks, persamaan AB dan BA bisa gagal untuk tiga alasan:
- AB dapat didefinisikan dan BA tidak dapat didefinisikan (sebagai contoh, jika A berukuran 2 x 3 dan B adalah 3 x 4).
- AB dan BA keduanya dapat didefinisikan, tetapi mereka mempunyai ukuran yang berbeda (misalnya, jika A berukuran 2 x 3 dan B berukuran 3 x 2).
- AB dan BA keduanya dapat didefinisikan dan mempunyai ukuran sama, tetapi dua perkalian tersebut dapat berbeda. (seperti diilustrasikan dalam contoh berikutnya).
Contoh 2:
Perhatikan matriks A dan B berikut ini.

Dengan perkalian memberikan

Dari dua perkalian matris tersebut jelas terlihat bahwa AB ≠ BA. Dalam kasus tertentu, anda mungkin menjumpai bahwa hasil dari dua perkalian tersebut memberikan nilai yang sama.
Sifat-sifat penting operasi matriks lainnya terkait dengan matriks nol. Berikut ini diberikan sifat-sifat dari matriks nol tersebut.
Teorema 2: Sifat-sifat Matriks Nol
Jika \(c\) adalah suatu skalar, dan jika ukuran matriks yang diberikan memungkinkan untuk dapat melakukan operasi matriks, maka:
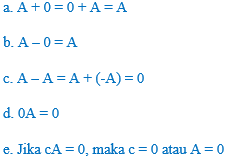
Karena kita tahu bahwa hukum komutatif dari aritmatika riil adalah tidak valid dalam aritmatika matriks, maka tidak mengherankan jika ada aturan lain yang gagal juga. Sebagai contoh, perhatikan dua hukum aritmatika riil berikut ini:
- Jika ab = ac dan a ≠ 0, maka b = c. (Hukum Cancellation)
- Jika ab = 0, maka setidaknya salah satu faktor pada ruas kiri adalah nol.
Dua contoh selanjutnya akan menunjukkan bahwa hukum tersebut adalah tidak benar dalam aritmatika matriks.
Contoh 3:
Misalkan diketahui matriks A, B dan C sebagai berikut:

Perhatikan bahwa hasil kali AB sama dengan AC (AB = AC), yakni

Meskipun A ≠ 0, menggagalkan A dari dua sisi persamaan AB = AC akan menyebabkan kesimpulan yang tidak benar bahwa B = C (perhatikan bahwa matriks B ≠ C). Oleh karena itu, hukum cancellation tidak berlaku secara umum untuk perkalian matriks (walaupun mungkin saja terdapat kasus tertentu di mana hukum cancellation ini berlaku).
Contoh 4:
Diketahui matriks A dan B sebagai berikut.
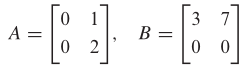
Perhatikan bahwa hasil kali AB = 0, tetapi A ≠ 0 dan B ≠ 0.
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
The best time to plant a tree was 20 years ago. The second best time is now.
