www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Matriks › Definisi Determinan Matriks
Matriks
Definisi Determinan Matriks
Determinan matriks mempunyai penerapan-penerapan penting dalam sistem persamaan linear dan mencari invers dari suatu matriks.
Determinan matriks mempunyai penerapan-penerapan penting dalam sistem persamaan linear dan mencari invers dari suatu matriks. Oleh karena itu, pemahaman mengenai determinan matriks ini adalah hal yang fundamental.
Dalam pelajaran matematika dasar saat sekolah menengah, kita mempelajari bahwa determinan suatu matriks berukuran 2 x 2, yaitu:

dan determinan matriks berukuran 3 x 3, yaitu
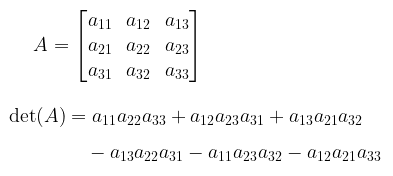
Teknik mencari determinan ini dikenal dengan metode Sorrus. Mungkin ada beberapa di antara kalian yang pernah bertanya darimana rumus tersebut diperoleh? Setelah Anda selesai membaca artikel ini, Anda akan bisa menjawab pertanyaaan tersebut.
Bagi yang tidak tertarik mengenai masalah pembuktian, silahkan abaikan saja tulisan berikutnya dari artikel ini karena pada dasarnya nanti kita akan sampai pada rumus yang sama dengan yang tertera di atas.
Mari kita mulai dengan mengingat kembali konsep mengenai permutasi. Dari konsep permutasi ini nanti kita akan sampai pada pengertian mengenai determinan matriks.
Permutasi
Permutasi himpunan bilangan-bilangan bulat {1, 2, . . . , n} adalah susunan bilangan-bilangan bulat ini menurut suatu aturan tanpa menghilangkan atau mengulangi bilangan-bilangan tersebut.
Sebagai contoh, ada enam permutasi yang berbeda dari himpunan bilangan-bilangan bulat {1, 2, 3}. Permutasi-permutasi ini adalah:

Dari contoh ini kita lihat bahwa ada 6 permutasi dari {1, 2, 3}. Umumnya, himpunan {1, 2, 3, . . . , n} akan mempunyai

permutasi yang berbeda. Dalam Contoh di atas, n = 3, sehingga akan mempunyai \(3! = 6\) permutasi.
Inversi (inversion)
Untuk menyatakan permutasi umum dari himpunan {1, 2, . . . , n}, maka kita akan menuliskan (j1, j2 , . . . , jn). Di sini, j1 adalah bilangan bulat pertama dalam permutasian, j2 adalah bilangan kedua, dan seterusnya. Sebuah inversi dikatakan terjadi dalam permutasi (j1, j2 , . . . , jn ) jika sebuah bilangan bulat yang lebih besar mendahului sebuah bilangan bulat yang lebih kecil.
Jumlah inversi seluruhnya yang terjadi dalam permutasi dapat diperoleh sebagai berikut: (1) carilah banyaknya bilangan bulat yang lebih kecil dari j1 dan yang membawa j1 dalam permutasi tersebut; (2) carilah banyaknya bilangan bulat yang lebih kecil dari j2 dan yang membawa j2 dalam permutasi tersebut. Teruskanlah proses penghitungan ini untuk j3 , . . . , j(n-1). Jumlah bilangan-bilangan ini akan sama dengan jumlah inversi seluruhnya dalam permutasi tersebut.
Contoh 2: Inversi
Tentukanlah banyaknya inversi dalam permutasi-permutasi berikut: (i) (6, 1, 3, 4, 5, 2), (ii) (2, 4, 1, 4), (iii) (1, 2, 3, 4)
Pembahasan:
- Banyaknya inversi adalah 5 + 0 + 1 + 1 + 1 = 8
- Banyaknya inversi adalah 1 + 2 + 0 = 3.
- Tidak ada inversi dalam permutasi ini.
Permutasi Genap dan Permutasi Ganjil
Sebuah permutasi dinamakan genap (even) jika jumlah inversi seluruhnya adalah sebuah bilangan bulat yang genap dan dinamakan ganjil (odd) jika jumlah inversi seluruhnya adalah sebuah bilangan bulat yang ganjil.
Contoh 3:
Tabel berikut mengklasifikasikan berbagai permutasi dari \(\{1, 2, 3\}\) sebagai genap atau ganjil.

Hasil Kali Elementer
Tinjaulah matriks A berukuran \(n×n\) berikut ini.

Yang kita artikan sebagai hasil kali elementer A adalah setiap hasil kali n entri A, sedangkan dua di antaranya tidak boleh berasal dari baris yang sama atau dari kolom yang sama.
Contoh 4: Hasil Kali Elementer
Daftarkanlah semua hasil kali elementer dari matriks-matriks
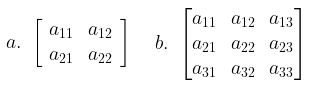
Pembahasan:
- Karena setiap hasil kali elementer mempunyai dua faktor, dan karena setiap faktor berasal dari baris yang berbeda, maka hasil kali elementer dapat dituliskan dalam bentuk
- karena setiap hasil kali elementer mempunyai tiga faktor, yang masing-masing berasal dari baris yang berbeda, maka hasil kali elementer dapat dituliskan dalam bentuk

di mana titik kosong menandakan nomor kolom. Karena tidak terdapat dua faktor dalam hasil kali tersebut berasal dari kolom yang sama, nomor kolom haruslah 1 2 atau 2 1. Maka, hasil kali elementer hanyalah \(a_{11}, a_{22}\) dan \(a_{12}, a_{21}\).

Karena tidak terdapat dua faktor dalam hasil kali tersebut berasal dari kolom yang sama, maka nomor kolom tidak mempunyai pengulangan; sebagai konsekuensinya, maka nomor kolom tersebut harus membentuk permutasi himpunan {1, 2, 3}. Di sini permutasi 3! = 6 menghasilkan daftar hasil kali elementer berikut.

Seperti yang ditunjukkan dalam Contoh di atas, matriks \(A\) yang berukuran \(n×n\) mempunyai \(n!\) hasil kali elementer. Hasil kali elementer tersebut adalah hasil kali yang berbentuk \(a_{{1j}_1}, a_{{2j}_2}, . . . , a_{{nj}_n}\), di mana \((j_1, j_2, . . . , j_n)\) adalah permutasi himpunan \(\{1,2,…,n\}\).
Hasil Kali Elementer Bertanda
Yang kita artikan dengan hasil kali elementer bertanda \(A\) adalah hasil kali elementer \(a_{{1j}_1}, a_{{2j}_2}, . . . , a_{{nj}_n}\) dikalikan dengan \(+1\) atau \(-1\). Kita gunakan tanda \(+\) jika \((j_1, j_2, . . . , j_n)\) adalah permutasi genap dan tanda \(–\) jika \((j_1, j_2, . . . , j_n)\) adalah permutasi ganjil.
Contoh 5: Hasil Kali Elementer Bertanda
Daftarkanlah semua hasil kali elementer bertanda dari matriks-matriks
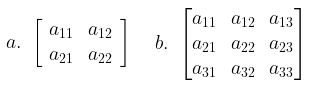
Pembahasan:
- Hasil kali elementer, permutasi terasosiasi, permutasi genap atau ganjil, dan hasil kali elementer bertanda diberikan pada tabel berikut:
- Hasil kali elementer, permutasi terasosiasi, permutasi genap atau ganjil, dan hasil kali elementer bertanda diberikan pada tabel berikut:


Kita sekarang sudah siap untuk mendefinisikan fungsi determinan.
Definisi determinan
Definisi: Determinasi
Misalkan \(A\) adalah matriks kuadrat. Fungsi determinan dinyatakan oleh \(\det\), dan kita definisikan \(\det(A)\) sebagai jumlah semua hasil kali elementer bertanda dari \(A\). Jumlah \(\det(A)\) kita namakan determinan \(A\).
Dengan melihat kembali ke Contoh 5, kita dapatkan
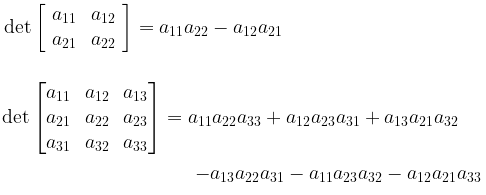
Untuk memudahkan teman-teman dalam mengingat rumus di atas perhatikanlah ilustrasi berikut.

Ilustrasi (a) memperlihatkan bahwa determinan matriks 2 x 2 dapat diperoleh dengan mengalikan entri-entri pada panah yang mengarah ke kanan dan mengurangkan hasil kali entri-entri pada panah yang mengarah ke kiri.
Sementara pada ilustrasi (b), kita menyalin kembali kolom pertama dan kolom kedua; kemudian menyandingkannya ke sebelah kanan matriks tersebut. Determinan matriks 3 x 3 tersebut kemudian dihitung dengan menjumlahkan hasil kali pada panah-panah yang mengarah ke kanan dan mengurangkan hasil kali pada panah-panah yang mengarah ke kiri.
Contoh 6: Menghitung Determinan
Hitunglah determinan-determinan dari matriks A berukuran 2 x 2 dan matriks B berukuran 3 x 3 berikut ini.

Penyelesaian:
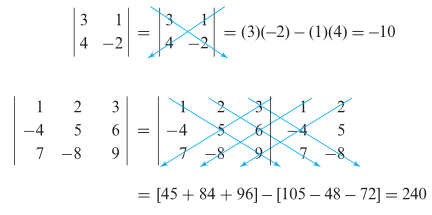
Notasi penulisan determinan
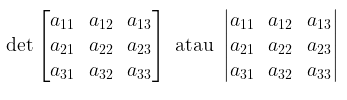
Kita simpulkan bagian ini dengan beberapa komentar mengenai terminologi dan notasi. Pertama, kita perlihatkan bahwa simbol \(|A|\) merupakan notasi alternatif untuk \(\det(A)\). Sebagai contoh, determinan matriks 3 x 3 dapat kita tulis sebagai
Misalkan kita punya matriks

Maka notasi determinan dapat dituliskan sebagai
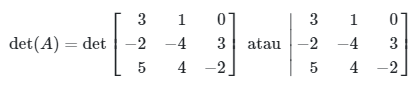
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
A pessimist sees the difficulty in every opportunity; an optimist sees the opportunity in every difficulty.
