www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Vektor & Ruang Vektor › Perkalian Titik dan Perkalian Silang Vektor: Materi, Contoh Soal dan Pembahasan
Perkalian Titik dan Perkalian Silang Vektor: Materi, Contoh Soal dan Pembahasan
Terdapat perbedaan penting antara hasil kali titik dan hasil kali silang dari dua vektor yakni hasil kali titik adalah suatu skalar dan hasil kali silang adalah suatu vektor.
Jika \(u\) dan \(v\) adalah vektor-vektor di ruang-2 dimensi atau ruang-3 dimensi dan \(θ\) adalah sudut di antara \(u\) dan \(v\), maka hasil kali titik (dot product) atau hasil kali dalam Euclidis (Euclidean inner product) didefinisikan sebagai berikut:

|
(1) |
Sekarang misalkan \(u=(u_1, u_2, u_3)\) dan \(v=(v_1, v_2, v_3)\) adalah dua vektor taknol. Jika \(θ\) adalah sudut di antara \(u\) dan \(v\) (Lihat Gambar 1), maka sesuai hukum cosinus diperoleh:
 |
(2) |
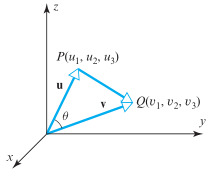
Gambar 1.
Karena \( \overrightarrow{PQ} = v-u \), maka dapat kita tuliskan kembali persamaan (2) sebagai

Dengan mensubstitusikan
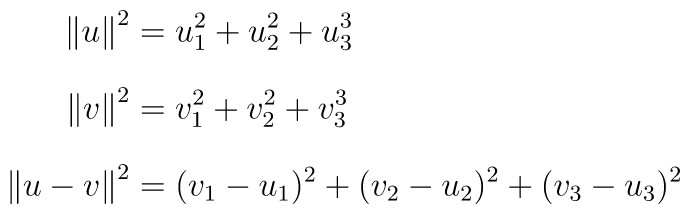
maka setelah dilakukan penyederhanaan, kita akan dapatkan:

Jika \(u=(u_1, u_2)\) dan \(v=(v_1, v_2)\) adalah dua vektor di ruang-2 dimensi, maka rumus yang bersesuaian adalah

Pada kasus khusus jika vektor \(u = v\), maka hasil kali titik antara \(u\) dan \(v\);

Jika \(u\) dan \(v\) adalah dua vektor taknol, maka dari rumus perkalian titik kita bisa mendapatkan sudut di antara kedua vektor tersebut, yakni:
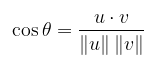
|
(3) |
Selanjutnya, teorema berikut akan memaparkan sifat-sifat penting dari hasil kali titik vektor. Hasil kali titik ini akan bermanfaat dalam penghitungan yang mencakup vektor-vektor.
Teorema:
Jika \(u\), \(v\) dan \(w\) adalah vektor-vektor di ruang-2 atau ruang-3 dan \(k\) adalah skalar, maka
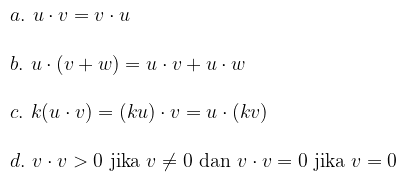
Teorema:
Misalkan \(u\) dan \(v\) adalah vektor di ruang-2 atau ruang-3.
- \( v⋅v = \left \| v \right \|^2 \), yakni \( \left \| v \right \| = (v⋅v)^{1/2} \)
- Jika \(u\) dan \(v\) adalah vektor-vektor taknol dan \(θ\) adalah sudut di antara kedua vektor tersebut, maka
\(θ\) lancip, jika dan hanya jika \( u⋅v > 0 \)
\(θ\) tumpul, jika dan hanya jika \( u⋅v < 0 \)
\(θ = \pi/2 \) , jika dan hanya jika \( u⋅v = 0 \)
Vektor tegaklurus disebut juga vektor ortogonal. Pada penjelasan Teorema di atas, dua vektor taknol adalah tegak lurus jika dan hanya jika hasil kali titiknya adalah nol. Jadi, dua vektor adalah tegak lurus jika dan hanya jika \(u \cdot v = 0\). Notasi \(u⊥v\) menyatakan bahwa \(u⋅v\) adalah vektor ortogonal.
Contoh Soal dan Pembahasan Perkalian Titik Vektor
Setelah memahami beberapa konsep dasar dan rumus berkaitan dengan perkalian titik vektor, sekarang kita akan masuk ke contoh soal berkaitan dengan perkalian titik vektor beserta pembahasannya.
Contoh 1:
Jika \(u = (1, -2,3)\), maka tentukan panjang vektor \(u\).
Pembahasan:
Panjang vektor \(u\) dapat ditentukan sebagai berikut:

Contoh 2:
Misalkan diketahui dua vektor \(u\) dan \(v\) sebagaimana diperlihatkan pada Gambar 1. Tentukan perkalian titik antara vektor \(u\) dan \(v\).

Gambar 1.
Pembahasan:
Dari gambar terlihat vektor \(u=(0,0,1)\) dan vektor \(v=(0,2,2)\) serta sudut di antara kedua vektor adalah 450. Dengan demikian, berdasarkan rumus perkalian titik, didapatkan hasil berikut:

Contoh 3:
Tinjaulah vektor-vektor \(u = (2, -1, 1)\) dan \(v = (1, 1, 2)\). Carilah \(u⋅v\) dan tentukanlah sudut \(θ\) di antara \(u\) dan \(v\).
Penyelesaian:
Ingat bahwa:
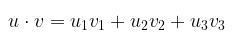
Untuk vektor yang diberikan kita dapatkan panjang vektornya yaitu \(\left \| u \right \|=\left \| v \right \|=\sqrt{6}\), sehingga dari persamaan (3), kita peroleh
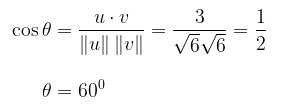
Contoh 4:
Jika \(u = (1, -2, 3)\), \(v = (-3, 4, 2)\), dan \(w = (3, 6, 3)\), maka

Dengan demikian, \(u\) dan \(v\) membentuk sudut tumpul, \(v\) dan \(w\) membentuk sudut lancip, dan \(u\) serta \(w\) tegak lurus satu sama lain.
Hasil Kali Silang
Definisi:
Jika \(u=(u_1, u_2, u_3)\) dan \(v=(v_1, v_2, v_3)\) adalah vektor di ruang-3 dimensi, maka hasil kali silang \(u × v\) adalah vektor yang didefinisikan oleh

atau dalam notasi determinan

Hasil perkalian vektor silang \(u \times v\) adalah berupa suatu vektor di mana tiap sel-nya merupakan hasil determinan. Determinan sel pertama diperoleh dengan membuang kolom (atau baris) pertama dari matriks, determinan sel kedua diperoleh dengan membuat kolom (atau baris) kedua dari matriks dan determinan sel ketiga dengan cara membuang kolom (atau baris) ketiga dari matriks.
Contoh 5:
Carilah \(u \times v\), di mana \(u = (1,2,-2)\) dan \(v = (3,0,1)\).
Penyelesaian:


Hubungan perkalian titik dan perkalian silang
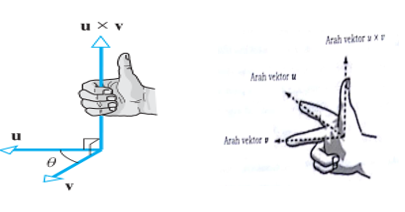
Terdapat perbedaan penting antara hasil kali titik dan hasil kali silang dari dua vektor yakni hasil kali titik adalah suatu skalar dan hasil kali silang adalah suatu vektor. Hubungan penting antara hasil kali titik dan hasil kali silang \(u \times v\), menunjukkan bahwa \(u \times v\) adalah ortogonal terhadap \(u\) maupun terhadap \(v\). (Perhatikan kaidah tangan kanan pada gambar di bawah bahwa \(u \times v\) tegak lurus baik terhadap \(u\) maupun \(v\))
Definisi:
Jika \(u\) dan \(v\) adalah vektor di ruang-3, maka:

Contoh 6:
Tinjaulah vektor \( u = (1, 2, -2) \) dan \( v = (3, 0, 1) \). Kita telah menampilkan pada Contoh 5 bahwa

karena

dan
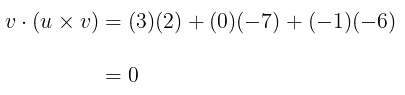
maka, \(u \times v\) ortogonal baik untuk \(u\) maupun \(v\) seperti ditunjukkan oleh Teorema 5.
Teorema:
Jika \(u, v\) dan \(w\) adalah sebarang vektor di ruang-3 dimensi dan \(k\) adalah sebarang skalar, maka:

Dapat diketahui dari teorema di atas bahwa \(u \times v\) ortogonal terhadap kedua vektor \(u\) dan \(v\). Jika vektor \(u\) dan \(v\) adalah vektor taknol, dapat ditunjukkan bahwa arah \(u \times v\) dapat ditentukan menggunakan “aturan tangan kanan”. Jika dimisalkan vektor u adalah jari telunjuk, dan vektor \(v\) adalah jari tengah dari tangan kanan kita, maka hasil perkalian silang \(u \times v\) adalah suatu vektor yang arahnya seperti ibu jari tangan kanan.
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Watch your thoughts; they become words. Watch your words; they become actions. Watch your actions; they become habits. Watch your habits; they become character. Watch your character; it becomes your destiny.
