www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Matriks › Sifat Determinan
Sifat Determinan
Mengetahui sifat-sifat terkait determinan akan membantu kita dalam menghitung determinan dengan lebih cepat, karena sering kali matriks tertentu mempunyai bentuk yang memudahkan kita dalam menghitung determinannya.
Pada artikel ini kita akan membahas sifat-sifat determinan matriks. Mengetahui sifat-sifat terkait determinan akan membantu kita dalam menghitung determinan matriks dengan lebih cepat, bahkan adakalanya hanya dengan melihat saja kita bisa menemukan determinan matriks tersebut tanpa perlu melakukan penghitungan di kertas. Ini bisa dilakukan karena sering kali matriks tertentu mempunyai bentuk yang memudahkan kita dalam menghitung determinannya.
Sifat-sifat determinan matriks tersebut akan dituangkan dalam teorema-teorema berikut.
Teorema 1:
Jika A adalah sebarang matriks kuadrat di mana terdapat baris yang entri-entri pada baris tersebut semuanya mengandung sebarang bilangan nol, maka det(A) = 0.
Contoh 1: Determinan Matriks
Diketahui matriks A sebagai berikut.
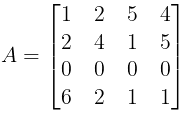
Determinan dari matriks A adalah nol (det(A) = 0), karena entri-entri pada baris ketiga dari matriks A berisi nol.
Teorema 2:
Jika A adalah matriks segitiga bawah atau matriks segitiga atas berukuran \(n × n\), maka det(A) adalah hasil kali entri-entri pada diagonal utama; yakni, \(\det(A) = a_{11} a_{22}⋅⋅⋅a_{nn}\).
Contoh 2:
Diketahui matriks segitiga atas sebagai berikut:

Determinan dari matriks A adalah:
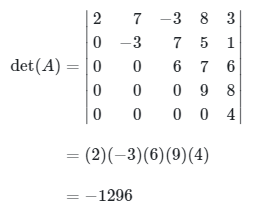
Teorema berikutnya akan memperlihatkan bagaimana operasi baris elementer pada matriks akan mempengaruhi nilai determinannya.
Teorema 3:
Misalkan \(A\) adalah sebarang matriks \(n×n\).
- Jika \(A’\) adalah matriks yang dihasilkan bila baris tunggal \(A\) dikalikan oleh konstanta \(k\), maka \(\det (A’) = k \det(A)\). Jika semua baris matriks \(A\) berukuran \(n×n\) dikalikan oleh konstanta \(k\), maka kita dapatkan \(\det(kA) = k^n \det(A)\).
- Jika \(A’\) adalah matriks yang dihasilkan bila dua baris \(A\) dipertukarkan, maka \(\det(A’) = - \det(A)\).
- Jika \(A’\) adalah matriks yang dihasilkan bila kelipatan satu baris \(A\) ditambahkan pada baris lain, maka \(\det(A’) = \det(A)\)
- Jika \(A\) adalah suatu matriks yang mempunyai dua baris atau dua kolom yang sebanding, maka \(\det(A) = 0\).
Contoh 3:
Tinjaulah matriks-matriks berikut.

Jika kita hitung determinan matriks-matriks ini dengan metode Sorrus yang telah kita pelajari, maka kita dapatkan

Perhatikanlah bahwa \(A_1\) kita dapatkan dengan mengalikan baris pertama \(A\) dengan 4; \(A_2\) kita dapatkan dengan mempertukarkan kedua baris pertama; dan \(A_3\) kita dapatkan dengan menambahkan – 2 kali baris ketiga \(A\) pada baris kedua. Seperti yang dinyatakan oleh Teorema 3, kita punyai hubungan

Contoh 4: Determinan Matriks
Tinjaulah matriks-matriks

Dengan perhitungan langsung maka \(\det(A) = 4\) dan \(\det(5A) = 100\). Ini sesuai dengan hubungan pada Teorema 3 bagian (a), yang menetapkan bahwa \(\det(5A) = 5^2 \det(A)\).
Contoh 5: Determinan Matriks
Berdasarkan Teorema 3 bagian (d), maka matriks

mempunyai determinan sebesar nol karena kolom pertama sebanding dengan kolom kedua.
Contoh 6: Determinan Matriks
Hitunglah \(\det(A)\), di mana

Pada matriks \(A\), kita menambahkan baris kedua dengan -2 kali baris pertama, sehingga diperoleh

Kita tidak memerlukan reduksi selanjutnya karena dari Teorema 1 kita peroleh bahwa \(\det(A) = 0\).
Dari contoh 5 dan 6 seharusnya sudah jelas bahwa apabila matriks kuadrat mempunyai dua baris yang sebanding (seperti baris pertama dan baris kedua \(A\)), maka kita akan memperoleh sebuah baris yang terdiri dari bilangan nol dengan menambahkan kelipatan yang sesuai dari salah satu baris ini pada baris yang satu lagi. Jadi, jika matriks kuadrat mempunyai baris yang sebanding, maka determinannya sama dengan nol.
Teorema 4:
Jika \(A\) dan \(B\) adalah matriks kuadrat yang ukurannya sama, maka \(\det(AB) = \det(A)⋅\det(B)\).
Contoh 7: Determinan Matriks
Tinjaulah matriks-matriks

Kita peroleh det(A) ⋅ det(B) = (1)(-23) = -23. Dengan penghitungan langsung maka det(AB) = -23, sehingga det(AB) = det(A) ⋅ det(B).
Perlu untuk ditekankan di sini bahwa biasanya det(A+B) tidaklah sama hasilnya dengan det(A) + det(B) atau dengan kata lain det(A + B) ≠ det(A) + det(B). Mari kita lihat contoh berikut:
Contoh 8: Determinan Matriks
Tinjaulah matriks-matriks
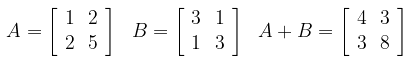
Kita peroleh \(\det(A) =1, \ \det(B) = 8\), dan \(\det(A + B) = 23\); jadi

Teorema 5:
Jika \(A\) adalah sebarang matriks kuadrat, maka \(\det(A) = \det(A^t)\).
Teorema 6:
Misakan \(A, \ A'\), dan \(A''\) adalah matriks \(n×n\) yang hanya berbeda dalam baris tunggal, katakanlah baris ke \(r\), dan anggaplah bahwa baris ke \(r\) dari \(A''\) dapat diperoleh dengan menambahkan entri-entri yang bersesuaian dalam baris ke \(r\) dari \(A\) dan dalam baris ke \(r\) dari \(A'\). Maka

Hasil yang serupa berlaku untuk kolom-kolom itu.
Contoh 9: Determinan Matriks
Misalkan diketahui matriks sebagai A sebagai berikut.
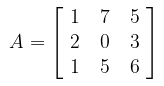
Dengan menghitung determinan, anda dapat memeriksa bahwa

Teorema 7:
Sebuah matriks A kuadrat dapat dibalik jika dan hanya jika det(A) ≠ 0. Jika A dapat dibalik, maka

Contoh 10: Determinan Matriks
Karena baris pertama dan baris ketiga dari

sebanding, maka \(\det(A) = 0\). Jadi, \(A\) tidak dapat dibalik.
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
It is not because things are difficult that we do not dare; it is because we do not dare that they are difficult.
