Contoh 1: Nilai Eigen untuk Matriks Segitiga

Carilah nilai eigen dari matriks segitiga atas berikut

Pembahasan:

Mengingat bahwa determinan dari matriks segitiga adalah perkalian dari entri-entri pada diagonal utama, maka kita peroleh

Oleh karena itu, persamaan karakteristiknya adalah

dan nilai eigennya adalah

yang mana merupakan entri/elemen diagonal dari \(A\).

Contoh 2: Mencari Nilai Eigen dari Matriks Segitiga

Carilah nilai-nilai eigen dari matriks segitiga bawah berikut:

Pembahasan:

Sebenarnya tanpa perlu melakukan perhitungan, Anda sudah bisa menebak bahwa nilai-nilai eigen dari matriks segitiga tersebut sama dengan diagonal matriksnya. Akan tetapi, kita akan membuktikannya dengan melakukan perhitungan berikut. Pertama kita cari dulu matriks \((λI-A)\), yaitu

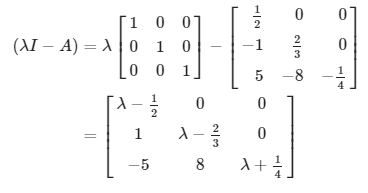
Determinan matriks segitiga adalah hasilkali elemen-elemen diagonal utama, sehingga

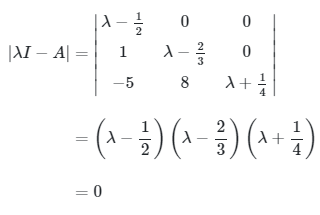
dan nilai eigennya adalah

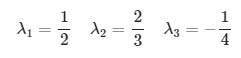
yang mana merupakan entri/elemen diagonal dari \(A\).