www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Bentuk Kuadratik › Bentuk Kuadratik: Materi, Contoh Soal dan Pembahasan
Bentuk Kuadratik: Materi, Contoh Soal dan Pembahasan
Dalam beberapa kasus, bentuk kuadratik lebih mudah diterapkan ketika tidak memiliki suku-suku hasil kali silang, yaitu ketika matriks bentuk kuadratik adalah matriks diagonal.
Suatu bentuk kuadratik dengan \(n\) variabel \((x_1, x_2,…, x_n\)) adalah suatu ekspresi yang dapat ditulis sebagai

di mana \(A\) adalah suatu matriks \(n×n\) yang simetris. Matriks \(A\) disebut matriks bentuk kuadratik.
Definisi: Bentuk Kuadratik
Bentuk kuadrat dinyatakan sebagai berikut:

di mana koefisien-koefisien \(a_{ij}\) merupakan elemen-elemen dari bentuk kuadrat dalam variabel \((x_1, x_2,…, x_n\)).
Contoh 1:
Misalkan \( X = \left[ {\begin{array}{rr} x_1 \\ x_2 \\ \end{array} } \right] \) . Hitung \( X^TAX \) untuk matriks berikut.

Pembahasan:
- Bentuk kuadratik dari matriks A pada (a) adalah
- Bentuk kuadratik dari matriks A pada (b) adalah
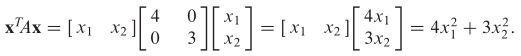
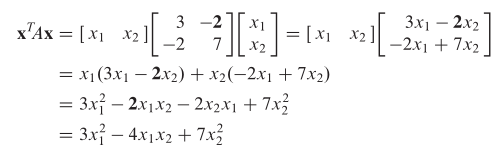
Kehadiran \(-4x_1x_2\) pada bentuk kuadratik bagian (b) disebabkan terdapat dua entri dengan nilai -2 dari diagonal pada matriks A. Sebaliknya, bentuk kuadratik yang berkaitan dengan matriks diagonal A pada (a) tidak mempunyai bentuk perkalian silang \( x_1x_2 \).
Contoh 2:
Diketahui persamaan:

Nyatakanlah bentuk kuadratik tersebut dalam bentuk \( X^TAX \).
Pembahasan:
Matriks bentuk tersebut boleh dituliskan dalam banyak cara tergantung pada bagaimana suku hasilkali silang \(-4x_1 x_2\) dan \(8x_1 x_3\) dipisahkan untuk membentuk suku-suku \(a_{12}x_1 x_2, a_{21} x_2 x_1\) dan \(a_{13} x_1 x_3, a_{31} x_1 x_3\).
Karena matriks dari bentuk kuadratik adalah matriks yang simetri maka suku-suku hasil kali silang \(a_{ij} = a_{ji}\). Sehingga,
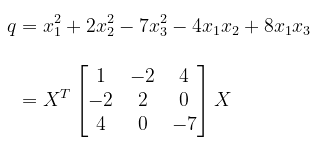
Contoh 3:
Diketahui \( Q(x) = x_1^2-8x_1x_2-5x_2^2 \). Hitung nilai \( Q(x) \) untuk
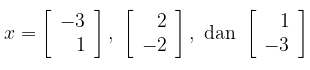
Pembahasan:

Perubahan Variabel dalam Bentuk Kuadratik
Dalam beberapa kasus, bentuk kuadratik lebih mudah digunakan ketika mereka tidak memiliki suku-suku hasilkali silang — yaitu, ketika matriks bentuk kuadratik adalah matriks diagonal. Untungnya, suku-suku hasilkali silang dapat dihilangkan dengan membuat perubahan variabel yang sesuai.
Jika \(x\) menyatakan vektor variabel dalam \(R^n\), maka perubahan variabel adalah sebuah persamaan dalam bentuk
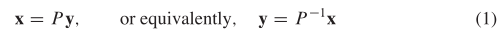
di mana \(P\) adalah matriks yang dapat dibalik dan \(y\) adalah sebuah vektor variabel baru pada \(R^n\).
Jika perubahan variabel (1) dilakukan pada bentuk kuadratik \(X^T AX\), maka
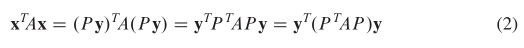
dan matriks baru bentuk kuadratik tersebut adalah \(P^T AP\). Karena \(A\) adalah simetris, maka terdapat matriks ortogonal \(P\) sedemikian sehingga \(P^T AP\) adalah matriks diagonal \(D\), dan bentuk kuadratik pada (2) menjadi \(y^T Dy\). Perhatikan contoh berikut ini.
Contoh 4:
Lakukanlah perubahan variabel yang mentransformasi bentuk kuadratik pada Contoh 3 menjadi bentuk kuadratik baru tanpa hasil kali silang.
Pembahasan:
Matriks bentuk kuadratik pada Contoh 3 adalah

Langkah pertama adalah mendiagonalisasi secara ortogonal matriks \(A\). Nilai eigen untuk matriks \(A\) adalah \(λ=3\) dan \(λ=-7\). Vektor eigen yang bersesuaian dengan nilai eigen tersebut adalah
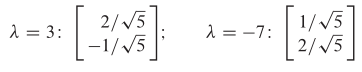
Vektor-vektor ini ortogonal secara otomatis (karena mereka mempunyai nilai eigen yang berbeda ) sehingga memberikan sebuah basis ortonormal untuk \(R^2\). Andaikan
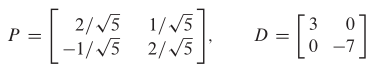
Maka \(A=PDP^{-1}\) dan \(D=P^{-1} AP=P^T AP\), seperti ditunjukkan sebelumnya. Perubahan variabelnya adalah

Dengan demikian,
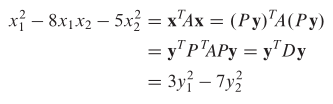
Untuk mengilustrasikan makna kesamaan bentuk kuadratik dalam Contoh 4, kita bisa menghitung \(Q(x)\) untuk \(x = (2,-2)\) menggunakan bentuk kuadratik baru. Pertama, karena \(x = Py\),
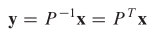
Sehingga

Dengan demikian,
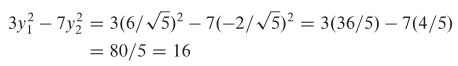
Ini adalah nilai \(Q(x)\) dalam Contoh 3 ketika \(x = (2, -2)\). Lihat gambar 1 berikut ini.

Gambar 1. Perubahan variabel \(X^T AX\)
Contoh 4 memberikan teorema berikut ini.
Teorema: Teorema Sumbu Utama
Andaikan \(A\) adalah matriks simetris n x n. Maka terdapat suatu perubahan variabel yang ortogonal, \(x = Py\), yang mentransformasi bentuk kuadratik \(X^T AX\) menjadi bentuk kuadratik \(y^T Dy\) tanpa suku-suku hasilkali silang.
Kolom-kolom matriks \(P\) dalam teorema tersebut disebut sumbu-sumbu utama (principal axes) bentuk \(X^T AX\).
Pandangan Geometris Sumbu Utama (A Geometric View of Principal Axes)
Misalkan \(Q(x)=X^T AX\), di mana \(A\) adalah matriks simetris 2 x 2 yang dapat dibalik, dan andaikan \(c\) adalah sebuah konstanta. Bisa ditunjukkan bahwa himpunan semua \(x\) dalam \(R^2\) yang memenuhi
\[ X^TAX = c \qquad \qquad (3) \]
akan mempunyai bentuk berupa elips (atau lingkaran), hiperbola, dua garis yang berpotongan, atau sebuah titik tunggal, atau tidak mempunyai titik sama sekali. Jika \(A\) adalah matriks diagonal, grafiknya berada dalam posisi standar, seperti pada Gambar 2.

Gambar 2. Sebuah elips dan hiperbola dalam posisi standar
Jika \(A\) bukan matriks diagonal, grafik persamaan (3) dirotasi terhadap posisi standar, seperti pada Gambar 3. Mencari sumbu-sumbu utama (yang ditentukan oleh vektor eigen \(A\)) sama dengan mencari sistem koordinat baru sehubungan dengan grafik pada posisi standar.

Gambar 3. Sebuah ellips atau hiperbola tidak dalam posisi standar
Hiperbola dalam Gambar 3(b) adalah grafik persamaan \(X^T AX=16\), di mana \(A\) adalah matriks dalam Contoh 4. Sumbu-\(y_1\) yang positif dalam Gambar 3(b) adalah menurut arah kolom pertama matriks P (in the direction of the first column of the matrix P) pada Contoh 4, dan sumbu-\(y_2\) positif adalah menurut arah kolom kedua matriks P.
Contoh 5:
Elips pada Gambar 3(a) adalah grafik persamaan \(5x_1^2-4x_1 x_2+5x_2^2=48\). Cari perubahan variabel yang menghilangkan suku hasilkali silang dari persamaan tersebut.
Pembahasan:
Matriks bentuk kuadratik adalah
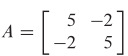
Nilai eigen dari matriks \(A\) yaitu 3 dan 7, dengan vektor eigen yang bersesuaian adalah

Andaikan

Maka P mendiagonalisasi secara ortogonal matriks \(A\), sehingga perubahan variabel \(x = Py\) menghasilkan bentuk kuadratik \(y^T Dy=3y_1^2+7y_2^2\). Sumbu-sumbu baru untuk perubahan variabel ini ditunjukkan dalam Gambar 3(a).
Mengklasifikasi Bentuk Kuadratik
Ketika \(A\) matriks n x n, bentuk kuadratik \(Q(x)=X^T AX\) adalah fungsi yang bernilai riil dengan domain \(R^n\). Gambar 4 menampilkan empat grafik bentuk kuadratik dengan domain \(R^2\).

Gambar 4. Grafik bentuk kuadratik
Contoh 2 x 2 dalam Gambar 4 memberikan kita ilustrasi definisi berikut:
Definisi:
Misalkan \(A\) matriks simetris, bentuk kuadratik \(Q(x) = X^TAX\) merupakan:
- Definit positif jika nilai \(X^TAX > 0\) untuk setiap \(X ≠ 0\)
- Semidefinit positif jika nilai \(X^TAX ≥ 0\) untuk setiap \(X\)
- Semidefinit negatif jika nilai \(X^TAX ≤ 0\) untuk setiap \(X\)
- Definit negatif jika nilai \(X^TAX < 0\)untuk setiap \(X ≠ 0\)
- Tak definit (indefinit) jika dan hanya jika A mempunyai nilai positif dan negatif.
Bentuk kuadratik pada bagian (a) dan (b) dari Gambar 4 adalah semidefinit positif, tetapi bentuk dalam (a) lebih baik digambarkan sebagai definit positif.
Teorema mencirikan beberapa bentuk kuadratik dalam hal nilai eigen.
Teorema: Bentuk Kuadratik dan Nilai Eigen
Andaikan A adalah matriks simetris n x n. Maka bentuk kuadratik \( X^TAX\) adalah
- definit positif jika dan hanya jika nilai eigen dari A semuanya positif,
- definit negatif jika dan hanya jika nilai eigen dari A semuanya negatif, atau
- Semidefinit positif jika dan hanya jika nilai eigen 0 dan positif
- Semidefinit negatif jika dan hanya jika nilai eigen 0 dan negatif
- tak definit (indefinit) jika dan hanya jika A mempunyai nilai eigen positif dan negatif.
Contoh 6: Bentuk Kuadratik
Dari matriks

dapat ditunjukkan bahwa matriks ini mempunyai nilai-nilai eigen \(λ = 2\) dan \(λ = 8\). Karena nilai-nilai eigen ini positif, maka matriks \(A\) definit positif, dan untuk semua \(x ≠ 0\)

Contoh 7: Bentuk Kuadrat
Apakah \(Q(x)=3x_1^2+2x_2^2+x_3^2+4x_1 x_2+4x_2 x_3\) adalah definit positif?
Pembahasan:
Karena mempunyai tanda positif semua, bentuk ini “tampaknya” adalah definit positif. Tapi matriks bentuk ini adalah

dan nilai eigen \(A\) ternyata adalah 5, 2, dan -1. Sehingga \(Q\) adalah bentuk kuadratik indefinit, bukan definit positif.
Teorema:
Suatu matriks simetris \(A\) definit positif jika dan hanya jika determinan dari setiap submatriks utamanya positif.
Contoh 8: Bentuk Kuadrat
Matriks
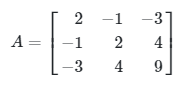
adalah definit positif karena
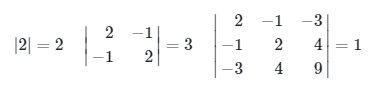
semuanya positif. Jadi, ada jaminan bahwa semua nilai eigen dari \(A\) positif dan \(X^TAX > 0\) untuk semua \(x ≠ 0\).
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
There are three things you can do with your life: You can waste it, you can spend it, or you can invest it. The best use of your life is to invest it in something that will last longer than your time on Earth.
