www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Matriks Kebalikan Umum › Definisi dan Teorema Matriks Kebalikan Umum
Definisi dan Teorema Matriks Kebalikan Umum
General inverse (g-inverse) atau matriks kebalikan umum memungkinkan kita untuk mencari invers suatu matriks yang tidak bujur sangkar atau determinannya sama dengan nol.
Jika sebuah matriks \(A\) yang berukuran \(n × n\) adalah matriks nonsingular, maka solusi dari suatu sistem persamaan linier \(Ax = g\) ada dan unik. Solusi persamaannya dapat dinyatakan sebagai \(x = A^{-1}g\), di mana \( A^{-1} \) adalah invers matriks A.
Jika Anda masih ingat bahwa invers matriks dapat dicari jika matriks tersebut adalah matriks yang bujur sangkar dan bersifat nonsingular yakni determinan dari matriks tersebut tidak sama dengan nol. Jika kondisi tersebut tidak terpenuhi maka kita tidak bisa mencari invers matriks tersebut.
Untungnya, terdapat cara lain yang memungkinkan kita untuk mencari invers suatu matriks dengan kondisi demikian. Kita namakan invers matriks yang diperoleh sebagai general inverse (g-inverse) atau matriks kebalikan umum (MKU). Kita definisikan matriks kebalikan umum sebagai berikut.
Definisi: Matriks Kebalikan Umum
Misalkan \(A\) adalah matriks berukuran \(m × n\). Jika matriks \(A^-\) ada dan memenuhi kondisi berikut, yakni
- \(AA^-\) dan \( A^-A \) adalah matriks simetris
- \( AA^-A = A \)
- \( A^-AA^- = A^- \)
Maka \(A^-\) disebut matriks kebalikan umum (MKU) atau general inverse dari \(A\). General inverse biasa dinyatakan sebagai g-inverse.
Contoh 1: Matriks Kebalikan Umum
Misalkan diketahui matriks

Matriks kebalikan umum (g-invers) dari matriks A di atas, yaitu:

(Kita akan membahas cara menghitung matriks kebalikan umum pada artikel berikutnya)
Dengan demikian, dari definisi matriks kebalikan umum, kita harus bisa membuktikan bahwa ketiga kondisi tersebut adalah benar. Berikut adalah pembuktian untuk kondisi pertama.
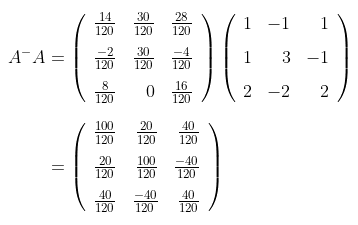

Perhatikanlah bahwa matriks \(AA^-\) dan \( A^-A \) adalah matriks yang simetris sehingga kondisi pertama terpenuhi.
Selanjutnya, kita akan membuktikan kondisi kedua dan ketiga, yakni


Jadi, ketiga kondisi terpenuhi sehingga \(A^-\) merupakan matriks kebalikan umum dari A.
Lalu, bagaimana kita menghitung matriks kebalikan umum ini? Sebelum kita menjawab pertanyaan ini, mari kita pelajari teorema-teorema terkait matriks kebalikan umum. Hal ini akan berguna dalam memudahkan penghitungan MKU pada pembahasan artikel kita berikutnya.
Teorema:
Untuk setiap matriks \(A\) terdapat matriks \(A^-\) yang memenuhi ketiga kondisi pada definisi MKU di atas; sehingga tiap matriks mempunyai g-invers.
Teorema:
Jika g-invers dari matriks \(A\) ukuran \(m × n\) ada, maka ukuran \(A^-\) nya adalah \(n × m\).
Teorema:
Jika \(A\) adalah matriks nol berukuran \(m × n\), maka \(A^-\) adalah matriks nol berukuran \(n × m\).
Teorema:
Untuk setiap matriks \(A\) terdapat matriks \(A^-\) yang unik yang memenuhi syarat pada persamaan (1), sehingga tiap matriks \(A\) memiliki g-invers yang unik.
Teorema:
Setiap g-invers dari transpos matriks \(A\) sama dengan transpos dari g-invers matriks \(A\), yaitu \((A^T)^- = (A^-)^T\).
Teorema:
g-invers dari \(A^-\) sama dengan \(A\), yaitu \((A^-)^- = A\).
Teorema:
Rank dari g-invers \(A\) sama dengan rank \(A\). Akibatnya, jika rank matriks \(A\) sama dengan \(r\), maka rank setiap matriks berikut juga sama dengan \(r\), yaitu

Teorema:
Untuk sebarang matriks \(A\): \((A^TA)^- = A^-(A^T)^-\).
Teorema:
Untuk sembarang matriks \(A\): \((AA^-)^- = AA^-\) dan \((A^-A)^- = A^-A\).
Teorema:
Misal \(P\) adalah matriks ortogonal berukuran \(m × m\), \(Q\) adalah matriks ortogonal berukuran \(n × n\) dan \(A\) sebarang matriks berukuran \(m×n\), maka \((PAQ)^-=Q^TA^-P^T\).
Teorema:
Jika\(A\) adalah matriks simetris, maka g-invers matriks \(A\) juga simetris; sehingga jika \(A=A^T\) maka \(A^- = (A^-)^T\).
Teorema:
Jika \(A = A^T\) maka \(AA^- = A^-A\).
Teorema:
Jika \(A\) adalah matriks nonsingular, maka \(A^-=A^{-1}\).
Teorema:
Jika \(A\) adalah matriks idempotent yang simetris maka \(A^-=A\); sehingga jika \(A = A^T\) dan \(A = A^2\), maka \(A^- = A\).
Teorema:
Misal \(D\) adalah matriks diagonal ukuran \(n × n\) dengan elemen \(d_{ii}, \ i = 1, 2, 3,…, n \ \). g-invers matriks \(D\) yaitu \(D^-\) adalah matriks diagonal dengan elemen diagonal ke-i dari \(D^-\) sama dengan \(d_{ii}^-\) jika \(d_{ii} ≠ 0\) dan sama dengan nol jika \(d_{ii} = 0\).
Teorema:
- Jika \(A\) matriks \(m×n\) adalah matriks dengan rank \(m\) maka \(A^- = A^T(AA^T)^1\) dan \(AA^- = I\). Jika rank \(A\) adalah \(n\), maka \(A^- = (A^TA)^- A^T\) dan \(A^-A = I\).
- Matriks \(AA^-, A^-A, I^-AA^-\) dan \(I^-A^-A\) semuanya merupakan matriks idempotent yang simetris.
- Jika \(B\) adalah matriks \(m×r\) dengan rank \(r(r > 0)\) dan \(C\) adalah matriks \(r × m\) dengan rank \(r\); maka \((BC)^- = C^-B^-\)
General Inverse untuk Matriks Khusus
Dalam kasus tertentu, matriks kebalikan umum (general inverse) dapat diperoleh dengan mudah untuk matriks tertentu atau matriks khusus. Berikut ini diberikan teorema-teorema terkait general inverse untuk matriks khusus.
Teorema:
- Jika \(c\) adalah skalar yang tidak nol, maka \((cA)^- = (1/c)A^-\).
- Jika \(A = A_1 + A_2 +⋯+ A_t\) dan \(A_i A_j^T = 0\) dan \(A_i^T A_j = 0\) untuk semua \(i, j = 1, 2,…, t; i ≠ j\), maka \(A^- = A_1^- + A_2^- +⋯+ A_t^-\).
- Misal \(A\) adalah sebarang matriks \(n × m\), misal \(K\) adalah matriks \(m×m\) yang nonsingular, dan misal \(B = AK\). Maka \(BB^-=AA^-\).
- Jika \(A^T A = AA^T\) maka \(A^-A = AA^-\) dan \((A^n)^- = (A^-)^n\) untuk setiap \(n\) bilangan bulat positif.
- Jika
- Jika \(A = B ⊗ C\), maka:
- Jika
- Jika \(a\) adalah vektor tak nol, maka \(a^- = (a^Ta)^- a^T\).
- Jika \(A\) adalah matriks berukuran \(m × n\) yang setiap elemennya sama dengan 1, maka:
- \(A^- = A^T\) jika dan hanya jika \(A^T A\) adalah idempoten (\(A = A^2\)).
\[ A = \left[ {\begin{array}{cc} B \\ C \\ \end{array} } \right] \]
dan \(BC^T = 0\), maka:


di mana \(B ⊗ C\) disebut kronecker product dari \(B\) dan \(C\)
\[ A = \left[ {\begin{array}{rr} B & 0 \\ 0 & C \\ \end{array} } \right] \]
maka
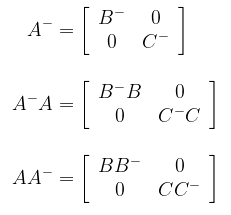
\[ A^- = \frac{1}{nm} A^T \]
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
The more you praise and celebrate your life, the more there is in life to celebrate.
