www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Diagonalisasi Matriks › Menghitung Pangkat Matriks Berdasarkan Diagonalisasi Matriks
Menghitung Pangkat Matriks Berdasarkan Diagonalisasi Matriks
Cara paling efisien untuk menghitung \(A^k\), khususnya untuk nilai \(k\) yang besar, adalah dengan mendiagonalkan matriks A. Masalah menghitung pangkat suatu matriks dapat dengan mudah disederhanakan apabila matriks tersebut dapat didiagonalisasi.
Dalam artikel sebelumnya, kita telah membahas sekilas mengenai nilai eigen dari pangkat suatu matriks. Kita akan mengulas kembali materi tersebut, dan kemudian kita akan menerapkannya untuk menghitung pangkat suatu matriks yang besar
Nilai Eigen dari pangkat suatu matriks
Cara yang paling efisien untuk menghitung \(A^k\), khususnya untuk nilai \(k\) yang besar, adalah pertama dengan mendiagonalkan \(A\).
Tetapi karena mendiagonalkan matriks \(A\) melibatkan pencarian nilai eigen dan vektor eigen, kita akan perlu untuk mengetahui bagaimana kuantitas ini berkaitan dengan itu dari matriks \(A^k\). Sebagai ilustrasi, anggaplah bahwa \(λ\) adalah nilai eigen dari \(A\) dan \(x\) adalah vektor eigen yang bersesuaian dengan \(λ\). Maka

yang mana menunjukkan tidak hanya bahwa \(λ^2\) adalah nilai eigen dari \(A^2\) tetapi bahwa \(x\) juga merupakan vektor eigen yang bersesuaian. Secara umum, kita mempunyai hasil berikut.
Teorema:
Jika \(k\) adalah bilangan bulat positif, \(λ\) adalah nilai eigen dari matriks \(A\), dan \(x\) adalah vektor eigen yang bersesuaian, maka \(λ^k\) adalah nilai eigen dari \(A^k\) dan \(x\) adalah vektor eigen yang bersesuaian.
Contoh 1:
Misalkan diketahui matriks

Carilah nilai eigen dan vektor eigen untuk matriks \(A^7\)!
Pembahasan:
Nilai eigen dan vektor eigen dari matriks A tersebut yaitu

Sehingga sesuai dengan teorema di atas maka nilai eigen dari matriks \(A^7\) yaitu \(λ=2^7=128\) dan \(λ=1^7=7\). Vektor-vektor eigen yang bersesuaian dengan \(λ=1\) dan \(λ=128\) sama dengan vektor-vektor eigen untuk matriks A.
Menghitung pangkat suatu matriks
Masalah menghitung pangkat suatu matriks dapat dengan mudah disederhanakan saat matriks tersebut dapat didiagonalisasi. Untuk melihat mengapa bisa demikian, anggaplah bahwa matriks \(A\) adalah sebuah matriks berukuran \(n×n\) yang dapat didiagonalisasi, sehingga \(P\) mendiagonalkan \(A\), dan bahwa

Dengan mengkuadratkan kedua ruas persamaan ini menghasilkan

Kita bisa menuliskan kembali ruas kiri persamaan ini sebagai
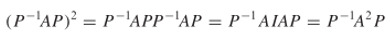
yang mana kita peroleh hubungan \(P^{-1}A^2P=D^2\). Secara lebih umum, jika \(k\) adalah bilangan bulat positif, maka penghitungan yang sama akan menunjukkan bahwa
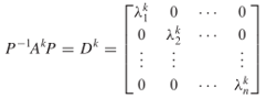
yang mana bisa kita tuliskan kembali sebagai

Contoh 2:
Gunakanlah persamaan (1) untuk mencari \(A^{13}\), di mana

Pembahasan:
Kita telah menunjukkan dalam Contoh 1 bahwa matriks \(A\) dapat didiagonalkan dengan

sehingga

Oleh karena itu, dari persamaan (1) kita peroleh:

Dari contoh di atas kita telah melihat bahwa kita bisa menghitung pangkat matriks yang besar ini dengan cukup cepat, tanpa bantuan kalkulator atau komputer. Dengan metode ini, pekerjaan besarnya adalah dalam mendiagonalkan \(A\). Sekali pekerjaan ini selesai, kita bisa menghitung setiap pangkat dari \(A\). Dengan demikian, untuk menghitung \(A^{1000}\) kita hanya perlu mengubah eksponen dari 13 menjadi 1000 dalam persamaan (2).
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
The more man mediates upon good thoughts, the better will be his world and the world at large.
