www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Sistem Persamaan Linear › Eliminasi Gauss-Jordan dan substitusi balik
Eliminasi Gauss-Jordan dan substitusi balik
Metode substitusi balik memungkinkan kita memecahkan suatu sistem persamaan linear menggunakan eliminasi Gauss untuk mengubah matriks yang diperbesar ke dalam bentuk eselon baris tanpa meneruskannya ke bentuk eselon baris tereduksi.
Pada artikel sebelumnya kita telah mempelajari prosedur yang mereduksi matriks menjadi bentuk eselon baris dan eselon baris tereduksi. Prosedur yang mereduksi matriks menjadi bentuk eselon baris tereduksi kita namakan eliminasi Gauss-Jordan, sementara prosedur mereduksi matriks hingga menghasilkan bentuk eselon baris kita namakan eliminasi Gauss.
Kita juga telah belajar bahwa jika matriks yang diperbesar untuk sistem persamaan linear dilakukan dasar-dasar operasi baris hingga menjadi bentuk eselon baris tereduksi, maka himpunan pemecahan untuk sistem tersebut dapat diperoleh dengan mudah.
Walaupun demikian, sering kali lebih memudahkan untuk memecahkan sistem persamaan linear dengan menggunakan eliminasi Gauss untuk mengubah matriks yang diperbesar ke dalam bentuk eselon baris tanpa meneruskannya ke bentuk eselon baris tereduksi. Bila ini dilakukan, maka sistem persamaan yang bersesuaian dapat dipecahkan dengan sebuah cara yang dinamakan substitusi balik (back-substitution).
Mari kita lihat sebuah contoh mereduksi matriks menjadi bentuk eselon baris tereduksi menggunakan eliminasi Gauss-Jordan. Kemudian kita akan menerapkan metode substitusi balik untuk contoh ini. Kita akan memperoleh hasil pemecahan sistem persamaan yang sama untuk kedua metode ini..
Contoh 1: Bentuk Baris Eselon Tereduksi
Pecahkanlah dengan menggunakan eliminasi Gauss-Jordan.

Matriks yang diperbesar untuk sistem tersebut adalah

Dengan menambahkan -2 kali baris pertama pada baris kedua dan baris keempat maka akan memberikan

Dengan mengalikan baris kedua dengan -1 dan kemudian menambahkan -5 kali baris kedua kepada baris ketiga dan -4 kali baris kedua kepada baris keempat maka akan memberikan

Dengan mempertukarkan baris ketiga dan baris keempat dan kemudian mengalikan baris ketiga dari matriks yang dihasilkan dengan 1/6 maka akan memberikan bentuk eselon baris

Dengan menambahkan – 3 kali baris ketiga pada baris kedua dan kemudian menambahkan 2 kali baris kedua dari matriks yang dihasilkan pada baris pertama maka akan menghasilkan bentuk eselon baris tereduksi.

Sistem persamaan-persamaan yang bersesuaian adalah

Dengan memecahkannya untuk peubah-peubah utama, maka kita dapatkan

Jika kita menetapkan nilai-nilai sebarang \(r, s\), dan \(t\) berurutan untuk \(x_2, x_4\), dan \(x_5\), maka himpunan pemecahan tersebut diberikan oleh rumus-rumus

Sekarang mari kita terapkan metode substitusi balik berdasarkan contoh yang diberikan di atas. Dari perhitungan dalam Contoh 1, bentuk eselon baris dari matriks yang diperbesar tersebut adalah

Untuk memecahkan sistem persamaan-persamaan yang bersesuaian

maka kita memrosesnya sebagai berikut:
Langkah 1. Pecahkanlah persamaan-persamaan tersebut untuk peubah-peubah utama.

Langkah 2. Mulailah dengan persamaan bawah dan bekerjalah ke arah atas, substitusikan secara keseluruhan masing-masing persamaan ke dalam semua persamaan yang di atasnya.

Dengan mensubstitusikan \(x_6=1/3\) ke dalam persamaan kedua maka akan menghasilkan

Langkah 3. Tetapkanlah nilai-nilai sebarang pada setiap peubah tak utama.
Jika kita menetapkan nilai-nilai sebarang \(r, s\), dan \(t\) berturut-turut untuk \(x_2, x_4\), dan \(x_5\), himpunan pemecahan tersebut diberikan oleh rumus-rumus

Mari kita lihat satu contoh lagi untuk memperkuat pemahaman terkait materi ini.
Contoh 2: Bentuk Baris Eselon Tereduksi
Carilah solusi atau penyelesaian dari persamaan berikut
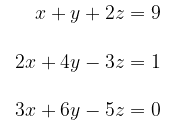
dengan menggunakan eliminasi Gauss dan substitusi balik.
Pembahasan.
Buatlah sistem persamaan tersebut menjadi matriks yang diperbesar, yaitu

kemudian reduksi matriks yang diperbesar tersebut menjadi bentuk eselon baris
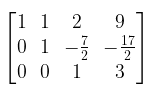
Sistem yang bersesuaian dengan matriks ini adalah
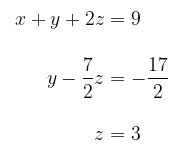
Dengan memecahkannya untuk peubah-peubah utama maka akan menghasilkan

Dengan mensubstitusikan persamaan bawah ke dalam persamaan-persamaan yang di atas maka akan menghasilkan
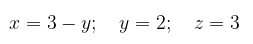
dan dengan mensubstitusikan persamaan kedua ke dalam persamaan atas maka akan menghasilkan
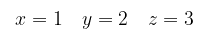
Hal ini sesuai dengan pemecahan yang kita peroleh dengan eliminasi Gauss-Jordan dalam Contoh 3.
Ketika kita melakukan dasar-dasar operasi baris pada matriks hingga menjadi bentuk eselon baris tereduksi, kita akan selalu mendapatkan matriks yang unik, yakni tidak peduli bagaimanapun dasar-dasar operasi baris tersebut diubah, kita akan selalu sampai pada bentuk eselon baris tereduksi yang sama.
Akan tetapi, bentuk eselon baris tidaklah unik, yakni dengan mengubah urutan dasar-dasar operasi baris tersebut maka kita mungkin sampai pada bentuk eselon baris yang berbeda.
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
In order to write about life first you must live it.
