www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Matriks › Teknik Mencari Invers Matriks
Teknik Mencari Invers Matriks
Jika A adalah matriks yang dapat dibalik, maka salah satu cara memperoleh invers matriks A yaitu dengan mengalikan kebalikan dari determinan matriks A terhadap adjoint matriks A tersebut.
Pada artikel sebelumnya kita telah belajar cara mencari determinan matriks menggunakan ekspansi kofaktor. Kita akan melanjutkan pembahasan tersebut untuk mencari invers dari suatu matriks. Mari kita review sekilas pembahasannya di sini:
Ekspansi Kofaktor
Jika \(A\) adalah matriks kuadrat, maka minor entri \(a_{ij}\) dinyatakan oleh \(M_{ij}\) dan didefinisikan menjadi determinan submatriks yang tetap setelah baris ke \(i\) dan kolom ke \(j\) dicoret dari \(A\). Bilangan \((-1)^{(i + j)} M_{ij}\) dinyatakan oleh \(C_{ij}\) dan dinamakan kofaktor entri \(a_{ij}\).
Contoh 1:
Misalkan terdapat matriks berikut.
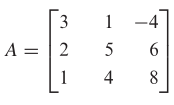
Tentukan minor entri dan kofaktor dari \(a_{11}\) dan \(a_{32}\).
Pembahasan:
Dari definisi yang diberikan di atas, maka minor entri \(a_{11}\) adalah
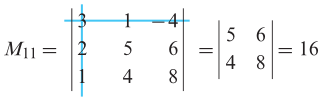
Dengan demikian, kofaktor \(a_{11}\) yaitu
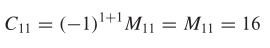
Demikian juga, minor entri \(a_{32}\) adalah

sehingga kofaktor \(a_{32}\) yaitu
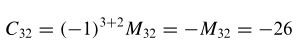
Perhatikan bahwa kofaktor dan minor elemen \(a_{ij}\) hanya berbeda dalam tandanya, yakni, \(C_{ij} = ±M_ij\). Cara cepat untuk menentukan apakah penggunaan tanda + atau tanda – merupakan kenyataan bahwa penggunaan tanda yang menghubungkan \(C_{ij}\) dan \(M_{ij}\) berada dalam baris ke \(i\) dan kolom ke \(j\) dari susunan

Misalnya, \(C_{ij}= M_{ij}, C_{21} = -M_{21}\), \(C_{12} = -M_{12}, C_{22} = M_{22}\), dan seterusnya.
Dengan demikian, determinan dari suatu matriks A dapat dicari dari salah satu persamaan berikut:

Sekarang, kita akan melanjutkan untuk mencari invers dari suatu matriks. Kita perlu mengenal satu istilah baru yang dinamakan adjoint. Perhatikan definisinya berikut ini.
Definisi: Adjoint
Jika \(A\) adalah sebarang matriks \(n × n\) dan \(C_{ij}\) adalah kofaktor \(a_{ij}\), maka matriks

dinamakan matriks kofaktor A. Transpos matriks ini dinamakan adjoin A dan dinyatakan adj(A).
Contoh 2: Mencari Invers Matriks
Misalkan

maka kofaktor A adalah
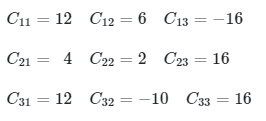
Sehingga matriks kofaktor nya adalah

dan adjoin A adalah

Kita sekarang sudah siap menghasilkan rumus untuk invers dari matriks yang dapat dibalik.
Teorema 1:
Jika A adalah matriks yang dapat dibalik, maka \[ A^{-1} = \frac{1}{\det(A)} \text{adj}(A) \]
Untuk Contoh 2 di atas, kita peroleh det(A) = 64. Dengan demikian, invers matriks A yaitu:
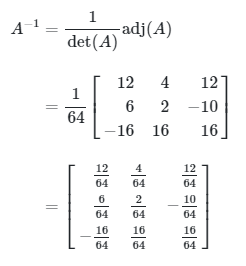
Kita perhatikan bahwa untuk matriks yang lebih besar dari \(3 × 3\) maka metode invers matriks dalam contoh ini secara perhitungan kurang ampuh. Oleh karena itu, kita akan mempelajari satu teknik lagi mengenai bagaimana mencari invers dari suatu matriks yaitu dengan menggunakan reduksi baris.
Metode Mencari Invers Matriks dengan Reduksi Baris
Untuk mencari invers matriks A yang dapat dibalik, kita harus mencari operasi baris elementer tereduksi A dan kemudian melakukan operasi yang sama ini pada \(I_n\) untuk mendapatkan \(A^{-1}\). Sebuah metode sederhana untuk melaksanakan prosedur ini diberikan dalam contoh berikut.
Contoh 4: Mencari Invers Matriks
Carilah invers dari

Pertama-tama, kita sandingkan matriks identitas yang ukurannya sama dengan matriks A di sebelah kanan matriks A \((A|I_n)\) seperti terlihat di bawah
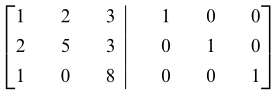 |
(1) |
Untuk mendapatkan invers matriks ini, kita akan melakukan operasi-operasi baris pada kedua ruas bentuk \(( A | I )\) menjadi bentuk \(( I |A^{-1} )\). Bagian terakhir dari pengoperasian baris ini akan menghasilkan invers matriks pada ruas kanan, dan matriks identitas pada ruas kiri. Mari kita lihat pengerjaannya di bawah ini.
Pada persamaan (1), kita menambahkan -2 kali baris pertama pada baris kedua dan -1 kali baris pertama pada baris ketiga. Sehingga diperoleh,
 |
(2) |
Pada persamaan (2), kita menambahkan 2 kali baris kedua pada baris ketiga, sehingga diperoleh
 |
(3) |
Pada persamaan (3), kita mengalikan baris ketiga dengan -1, diperoleh
 |
(4) |
Pada persamaan (4), kita menambahkan 3 kali baris ketiga pada baris kedua dan -3 kali baris ketiga pada baris pertama. Kita peroleh
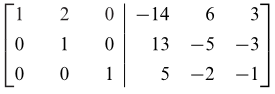 |
(5) |
Pada persamaan (5), kita menambahkan -2 kali baris kedua pada baris pertama.
 |
(6) |
Dengan demikian, invers dari matriks A yaitu

Sering tidak akan diketahui sebelumnya apakah sebuah matriks dapat dibalik. Jika matriks itu tidak dapat dibalik, maka, kita tidak akan memperoleh matriks identitas \(I_n\) pada ruas kiri, melainkan matriks berbentuk eselon baris tereduksi yang sedikit-dikitnya mempunyai sebuah baris bilangan nol.
Jadi, jika prosedur yang digunakan dalam contoh ini dicoba pada matriks yang tidak dapat dibalik, maka pada suatu tahap dalam perhitungan tersebut baris bilangan nol akan timbul pada ruas kiri. Dengan demikian, kita menyimpulkan bahwa matriks yang diberikan tidak dapat dibalik dan perhitungannya dapat dihentikan.
Contoh 5: Mencari Invers Matriks
Tinjaulah matriks

Dengan menerapakan prosedur dalam Contoh 4 akan diperoleh:
 |
(1) |
Pada persamaan (1), kita menambahkan -2 kali baris pertama ke baris kedua dan menambahkan baris pertama ke baris ketiga. Sehingga diperoleh
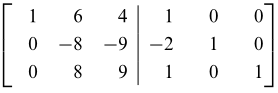 |
(2) |
Pada persamaan (2), kita menambahkan baris kedua ke baris ketiga. Sehingga diperoleh
 |
(3) |
Karena kita telah mendapatkan sebuah baris bilangan nol pada ruas kiri, maka matriks \(A\) tidak dapat dibalik.
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
It's up to you how far you go. If you don't try, you'll never know.
