Aljabar Linear   »   Sistem Persamaan Linear   ›  Matriks Eselon Baris dan Eselon Baris Tereduksi

Matriks Eselon Baris dan Eselon Baris Tereduksi

Suatu prosedur untuk mereduksi matriks menjadi bentuk eselon baris tereduksi dinamakan eliminasi Gauss-Jordan. Sedangkan, prosedur untuk mereduksi matriks sampai menjadi bentuk eselon baris dinamakan eliminasi Gauss.

Pada artikel ini kita akan mempelajari suatu prosedur yang sistematik untuk memecahkan sistem persamaan linear. Prosedur ini didasarkan pada gagasan untuk mereduksi matriks yang diperbesar (augmented matrix) menjadi bentuk yang cukup sederhana sehingga sistem persamaan tersebut dapat kita pecahkan dengan mudah.

Dalam bahasa lain, jika kita mempunyai sistem persamaan linear (SPL), katakanlah sistem persamaan linear dengan tiga variabel (x, y, dan z), maka untuk mencari solusi dari SPL tersebut atau menentukan nilai x, y, z; kita bisa buat SPL tersebut dalam bentuk matriks yang diperbesar (augmented matrix) .

Kemudian matriks tersebut direduksi menjadi bentuk eselon baris tereduksi. Dari matriks eselon baris tereduksi yang diperoleh, kita bisa langsung mendapatkan nilai x, y, dan z, yang merupakan solusi dari sistem persamaan linear tersebut.

Perhatikan contoh matriks diperbesar berikut ini yang telah dilakukan operasi-operasi baris dasar sehingga berada dalam bentuk eselon baris tereduksi (reduced row-echelon form)

Supaya berbentuk seperti ini, maka matriks tersebut harus mempunyai sifat-sifat berikut.

1. Jika baris dalam matriks tidak terdiri seluruhnya dari nol, maka bilangan tak nol pertama dalam baris tersebut adalah 1. Kita menamakan ini sebagai 1 utama.
2. Jika terdapat baris yang seluruh entri atau elemennya terdiri dari nol, maka semua baris dengan elemen-elemennya yang berupa nol tersebut dikelompokkan bersama-sama di bawah matriks.
3. Untuk dua baris berurutan yang seluruhnya elemennya tidak terdiri dari nol, maka 1 utama dalam baris yang lebih rendah diletakkan lebih jauh ke kanan dari 1 utama dalam baris yang lebih tinggi.
4. Masing-masing kolom yang mengandung 1 utama mempunyai elemen nol di tempat lain.

Sebuah matriks yang mempunyai sifat 1, 2, dan 3, dikatakan berada dalam bentuk eselon baris (row-echelon form), sedangkan matriks yang mempunyai semua sifat 1, 2, 3, dan 4 dikatakan berada dalam bentuk eselon baris tereduksi (reduced row-echelon form).

Pahamilah perbedaan antara matriks yang berada dalam bentuk eselon baris dan eselon baris tereduksi pada Contoh 1 di atas. Dari contoh tersebut, anda tentu bisa mengambil kesimpulan bahwa matriks dalam bentuk eselon baris harus mempunyai nol di bawah setiap 1 utama. Sedangkan matriks yang berada dalam bentuk eselon baris tereduksi harus mempunyai nol di atas dan di bawah masing-masing 1 utama.

Jika matriks yang diperbesar untuk sistem persamaan linear dilakukan dasar-dasar operasi baris hingga menjadi bentuk eselon baris tereduksi, maka himpunan pemecahan untuk sistem tersebut dapat diperoleh dengan mudah. Contoh berikut ini akan menunjukkan hal tersebut.

Dari Contoh 2 di atas, kita melihat bagaimana mudahnya memecahkan sistem persamaan linear jika matriks yang diperbesar tersebut berada dalam bentuk eselon baris tereduksi. Sekarang kita akan memberikan prosedur langkah demi langkah, yang dapat digunakan untuk mereduksi sebarang matriks menjadi bentuk eselon baris tereduksi. Misalkan matriks yang akan direduksi yaitu:

Langkah 1. Letakkanlah kolom paling kiri (garis vertikal) yang seluruhnya tidak terdiri dari nol.

Langkah 2. Pertukarkanlah baris atas dengan baris lain, jika perlu, untuk membawa entri tak nol ke atas kolom yang didapatkan dalam langkah 1.

Langkah 3. Jika entri yang sekarang ada di atas kolom yang didapatkan dalam Langkah 1 adalah a, kalikanlah baris pertama tersebut dengan 1/a untuk memperoleh 1 utama.

Langkah 4. Tambahkanlah kelipatan yang sesuai dari baris atas pada baris-baris yang di bawah sehingga semua entri di bawah 1 utama menjadi nol.

Langkah 5. Sekarang tutuplah baris atas dalam matriks tersebut dan mulailah sekali lagi dengan Langkah 1 yang diterapkan pada submatriks yang masih sisa. Teruskanlah dengan cara ini sampai entri matriks tersebut berada dalam bentuk eselon baris.

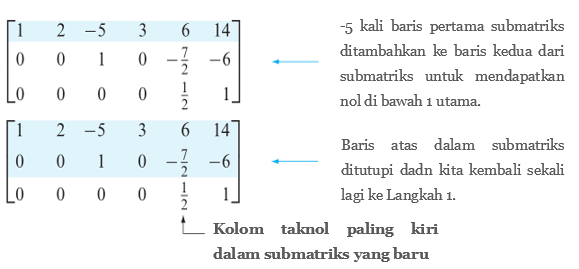
Entri matriks tersebut sekarang berada dalam bentuk eselon baris. Untuk mencari bentuk eselon baris tereduksi maka kita memerlukan langkah tambahan berikut.

Langkah 6. Dengan memulai dari baris tak nol terakhir dan bekerja ke arah atas, tambahkanlah kelipatan yang sesuai dari setiap baris pada baris-baris di atas untuk mendapatkan nol di atas 1 utama.

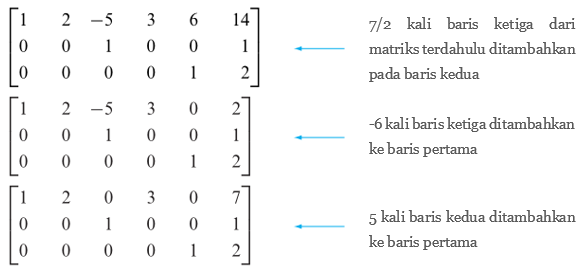
Matriks terakhir sudah berada dalam bentuk eselon baris tereduksi.

Prosedur di atas yang mereduksi matriks menjadi bentuk eselon baris tereduksi dinamakan eliminasi Gauss-Jordan. Jika kita hanya menggunakan lima langkah pertama, prosedur untuk menghasilkan bentuk eselon baris tersebut dinamakan eliminasi Gauss.

Sumber:

Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.