www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Matriks Kebalikan Umum › Menghitung Matriks Kebalikan Umum (General Inverse)
Menghitung Matriks Kebalikan Umum (General Inverse)
Secara umum, terdapat dua cara atau metode untuk memperoleh matriks kebalikan umum (general inverse) yakni metode penrose dan metode full-rank.
Secara umum, terdapat dua cara atau metode untuk memperoleh matriks kebalikan umum (general inverse atau g-inverse). Kedua metode tersebut adalah metode penrose dan metode full-rank. Kita akan membahas kedua metode tersebut pada artikel ini.
Metode Penrose
Misalkan matriks \(A\) berukuran \(n×n\) dan mempunyai rank \(r\). Jika determinan \(A\) tidak sama dengan nol (\(|A| \neq 0\)), maka g-inverse dapat dicari seperti halnya saat mencari invers biasa, \(A^- = A^{-1} \). Namun, jika determinan \(A\) sama dengan nol (\(|A| = 0\)), maka g-inverse dapat dicari dengan
\[ A^- = \frac{rC_rA^T}{tr(C_rB)} \]
Cara menghitung g-inverse ini dikenal sebagai metode penrose.
Langkah-langkah menghitungnya adalah sebagai berikut:
- Hitung \(B = A^TA\)
- \(C_1=I \)
- \( C_{i+1} = I⋅\left(\frac{1}{i}\right)⋅tr(C_rB)-C_1B \), untuk \( i=1,2,\dots,r-1 \)
- \( A^- = \frac{rC_rA^T}{tr(C_rB)} \)
Ada beberapa hal yang perlu diperhatikan terkait langkah-langkah di atas yakni: \( C_{r+1} = 0 \) dan \( tr(C_rB) \neq 0 \).
Untuk memahami penjelasan di atas, mari kita lihat beberapa contoh kasus berikut:
Contoh 1: Kasus determinan tidak sama dengan nol
Hitung g-inverse dari matriks berikut:

Pembahasan:
Karena \(\det(A)=1\), atau tidak sama dengan nol, maka g-inverse dari \(A = A^{-1}\). Cara mencari invers matriks ini telah kita pelajari. Dari hasil perhitungan diperoleh:

Contoh 2: Matriks berukuran \(n×n\)
Carilah g-inverse dari matriks berikut:
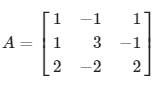
Pembahasan:
Dengan menggunakan langkah-langkah teorema di atas, kita peroleh
Langkah 1: Hitung matriks \( B= A^TA \), yakni

Langkah 2: Cari \( C_r \), yakni

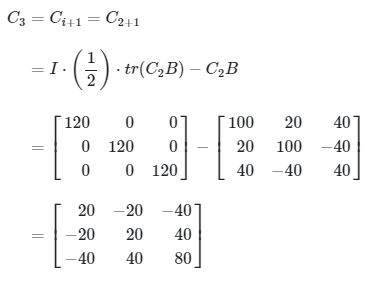
Perhatikan bahwa kita hanya menghitung sampai \( C_3 \) karena \(r\) tidak lebih besar dari 3 (r = 3) dan \( C_3B\neq0\)
Langkah 4: Hitung g-invers

Anda juga bisa menghitung g-inverse dari matriks berukuran \(m×n\) dengan metode penrose.
Contoh 3: Matriks berukuran \(m×n\)
Tentukan g-inverse dari matriks \(A\) berikut:

Dengan menggunakan langkah-langkah teorema di atas, kita peroleh
Langkah 1: Hitung matriks \( B= A^TA \), yakni

Langkah 2: Cari \( C_r \), yakni
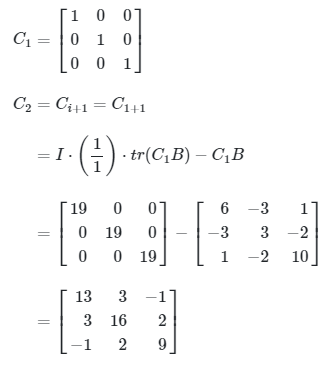

Perhatikan bahwa kita hanya menghitung sampai \( C_3 \) karena \(r\) tidak lebih besar dari 3 (r = 3) dan \( C_3B\neq0\)
Langkah 4: Hitung g-inverse

Metode Full Rank
Cara lain mencari matriks kebalikan umum (g-inverse) adalah menggunakan metode full rank. Untuk dapat menerapkan metode ini, perlu pemahaman mengenai rank suatu matriks. Konsep mengenai rank telah kita pelajari di artikel lain, sehingga kita tidak perlu menjelaskannya lagi di sini. Metode ini kita nyatakan dalam teorema berikut:
Teorema:
Untuk matriks \(A\) berukuran \(m×n\) dan full rank, maka g-inverse dapat dihitung sebagai berikut:
- Jika nilai rank sama dengan banyaknya baris (m), maka g-invers dapat dihitung dari rumus: \[ A^- = A^T (AA^T)^{-1} \]
- Jika nilai rank sama dengan banyaknya kolom (n), maka g-invers dapat dihitung dari rumus: \[ A^- = (A^TA)^{-1}A^T \]
Contoh 4: Kasus rank \(= m\)
Cari g-inverse dari matriks berikut:
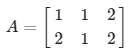
Pembahasan:
Karena \(r = 2\), maka berdasarkan teorema 2 di atas g-inverse dapat dicari dengan rumus:
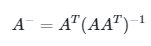
Dari hasil perhitungan diperoleh

Sistem Persamaan Linear
Teorema:
- Sistem persamaan linear \(Ax = g\) adalah konsisten jika dan hanya jika: \[ AA^-g = g \]
- Jika persamaan linear \(Ax = g\) mempunyai solusi, maka untuk setiap vektor \(h\) berukuran \(n×1\), vektor \(x\) merupakan solusi di mana: \[ x = A^-g + (I - A^-A) h \]
Contoh 5:
Tentukan apakah SPL berikut konsisten atau inkonsisten. Jika konsisten, cari vektor jawab (solusi) \(x_0 = A^-g + (I - A^-A) h\) untuk sembarang vektor \(h\) dari SPL tersebut ini.

Pembahasan:
Jika kita tulis persamaan SPL tersebut ke dalam bentuk \(AX = g\) maka,
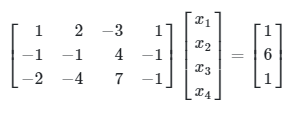
Matriks \(A\) mempunyai rank = 3 yang mana sama dengan banyaknya baris matriks \(A\) sehingga metode yang digunakan adalah full rank (baris) dengan rumus:

Dari hasil perhitungan diperoleh

Selanjutnya, untuk membuktikan apakah persamaan di atas konsisten, anda perlu untuk membuktikan apakah \(AA^-g = g\). Jika itu terpenuhi maka persamaan SPL di atas adalah konsisten. Dari pemeriksaan diperoleh

Jadi, terbukti bahwa \(AA^-g = g\).
Kemudian, untuk mencari solusi dari persamaan \(x_0 = A^-g + (I - A^-A) h\) dengan sembarang vektor \(h\), maka pertama anda harus memisalkan vektor \(h\) tersebut. Misalkan sembarang vektor \(h\) tersebut adalah (anda bisa menggunakan nilai sembarang vektor \(h\) lainnya):

Sehingga,


Dengan demikian,

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
As you know, life is an echo; we get what we give.
