Aljabar Linear   »   Sistem Persamaan Linear   ›  Operasi-operasi Baris Dasar

Operasi-operasi Baris Dasar

Terdapat tiga tipe operasi dasar yang sering digunakan untuk mencari penyelesaian atau solusi dari suatu sistem persamaan linear. Ketiga tipe operasi dasar tersebut dinamakan operasi baris elementer.

Terdapat tiga tipe operasi dasar yang sering digunakan untuk mencari penyelesaian atau solusi dari suatu sistem persamaan linear. Ketiga tipe operasi dasar tersebut yaitu:

1. Kalikanlah persamaan dengan konstanta yang tak sama dengan nol.
2. Pertukarkanlah dua persamaan tersebut.
3. Tambahkanlah kelipatan dari satu persamaan bagi yang lainnya.

Tiga tipe operasi dasar tersebut juga berlaku untuk matriks yang diperbesar (augmented matrix) karena baris dalam matriks yang diperbesar bersesuaian dengan persamaan dalam sistem yang diasosiasikan dengan baris tersebut, tetapi kita sekarang akan menggunakan kata baris daripada persamaan. Jadi ketiga tipe operasi dasar tersebut dapat dituliskan kembali menjadi:

1. Kalikanlah sebuah baris dengan sebuah konstanta yang tak sama dengan nol
2. Pertukarkanlah dua baris tersebut.
3. Tambahkanlah perkalian dari satu baris pada baris yang lainnya.

Operasi-operasi ini dinamakan operasi baris elementer. Contoh berikut menunjukkan bagaimana operasi itu dapat digunakan untuk memecahkan sistem-sistem persamaan linear.

Contoh 1:

Pada kolom sebelah kiri bawah, kita memecahkan sistem persamaan linear dengan mengoperasikannya pada persamaan dalam sisem tersebut, dan dalam kolom sebelah kanan kita memecahkan sistem yang sama dengan mengoperasikannya pada baris dari matriks yang diperbesar.

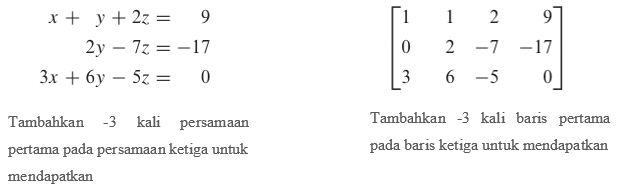
Pemecahan tersebut adalah \(x=1, y = 2, z = 3\).

Jadi, intinya adalah gunakan ketiga jenis operasi dasar yang telah dijelaskan di awal hingga membuat matriks yang diperbesar berbentuk matriks identitas jika kolom terakhirnya kita abaikan.

Sumber:

Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.