Aljabar Linear   »   Matriks Kebalikan Umum   ›  Matriks Partisi dan Matriks Kebalikan Umum

Matriks Partisi dan Matriks Kebalikan Umum

Untuk matriks yang berukuran besar, terkadang matriks kebalikan umum (g-inverse) dapat dicari dengan terlebih dahulu mempartisi matriks menjadi beberapa submatriks yang lebih kecil.

Matriks partisi adalah sebuah matriks yang diperoleh dari hasil pembagian matriks menjadi beberapa matriks yang mempunyai ukuran lebih kecil, yang disebut submatriks. Untuk matriks yang berukuran besar, mempartisi matriks membantu dalam menyederhanakan perhitungan, karena ukurannya lebih sederhana.

Hal ini bisa dilakukan karena beberapa sifat operasi matriks terpartisi mempunyai sifat seperti pada sifat operasi matriks biasa, misalnya penjumlahan dan perkalian dengan skalar. Walhasil, sifat-sifat lain seperti perkalian antara dua matriks terpartisi, determinan dan invers memiliki bentuk yang berbeda.

Matriks partisi

Definisi: Matriks partisi

Suatu matriks dapat dipartisi atau disekat dalam beberapa bagian berupa sub-matriks. Misalkan matriks \(A\) berukuran 3 x 3 yang dipartisi menjadi

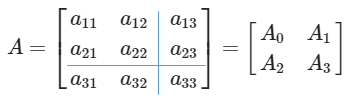
di mana

Matriks \( A_0, \ A_1, \ A_2, \ A_3 \) disebut sub-matriks dari matriks \( A \).

Sebagai contoh, berikut diberikan tiga partisi yang mungkin dari matriks \(A\) umum ukuran 3 x 4. Partisi pertama matriks \(A\) menjadi 4 submatriks \( A_{11}, A_{12}, A_{21} \), dan \( A_{22} \). Partisi kedua matris \(A\) menjadi vektor-vektor baris \( r_1, r_2 \), dan \( r_3 \); dan partisi ketiga matriks \(A\) menjadi vektor-vektor kolomnya \( c_1, c_2, c_3 \), dan \( c_4 \).

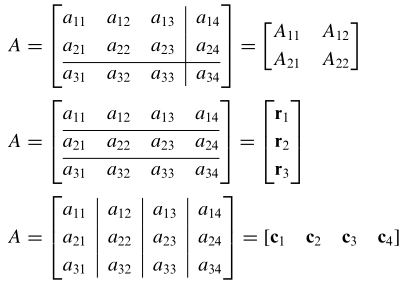
Matriks Partisi dan Matriks Kebalikan Umum

Dalam beberapa kasus, matriks kebalikan umum dapat dicari dengan terlebih dahulu mempartisi matriks menjadi beberapa submatriks yang lebih kecil. Matriks kebalikan umum kemudian diperoleh berdasarkan matriks kebalikan umum dari submatriks tersebut. Perhatikan teorema berikut.

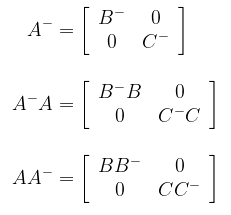
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.