www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Diagonalisasi Matriks › Diagonalisasi Matriks: Materi, Contoh Soal dan Pembahasan
Diagonalisasi Matriks: Materi, Contoh Soal dan Pembahasan
Matriks kuadrat A dikatakan dapat didiagonalisasi (diagonalizable) jika terdapat matriks P yang dapat dibalik sehingga \(P^{-1}AP\) diagonal; matriks P dikatakan mendiagonalisasi A.
Dalam banyak penerapan, mengetahui apakah suatu matriks kuadrat atau matriks persegi dapat didiagonalisasi merupakan hal yang penting, misalnya untuk menghitung pangkat suatu matriks yang besar.
Masalah Diagonalisasi Matriks
Diketahui matriks kuadrat \(A\), apakah terdapat matriks \(P\) yang dapat dibalik sehingga \(P^{-1} AP\) diagonal? Masalah ini menyarankan definisi berikut.
Definisi:
Matriks kuadrat \(A\) dikatakan dapat didiagonalisasi (diagonalizable) jika terdapat matriks \(P\) yang dapat dibalik sehingga \(P^{-1} AP\) diagonal; matriks \(P\) dikatakan mendiagonalisasi \(A\).
Teorema:
Jika \(A\) adalah matriks \(n×n\), maka pernyataan-pernyatan berikut ekivalen satu sama lain.
- \(A\) dapat didiagonalisasi.
- \(A\) mempunyai \(n\) vektor eigen yang bebas linear
Prosedur mendiagonalkan matriks \(A\) berukuran \(n×n\)
Berikut adalah prosedur untuk mendiagonalkan matriks \(A\) berukuran \(n×n\) yang dapat didiagonalisasi.
Langkah 1. Carilah \(n\) vektor eigen bebas linear \(A\), \(p_1,p_2,…,p_n\).
Langkah 2. Bentuklah matriks \(P\) yang mempunyai \(p_1,p_2,…,p_n\) sebagai vektor-vektor kolomnya.
Langkah 3. Matriks \(P^{-1} AP\) akan diagonal dengan \(λ_1,λ_2,…,λ_n\) sebagai entri-entri diagonalnya yang berurutan, di mana \(λ_i\) adalah nilai eigen yang bersesuaian dengan \(p_i,i=1,2,…n\).
Contoh 1: Diagonalisasi Matriks
Carilah matriks \(P\) yang mendiagonalkan

Pembahasan:
Nilai-nilai eigen dari matriks \(A\) adalah \(λ=1\) dan \(λ=5\). Adapun vektor-vektor berikut

membentuk sebuah basis untuk ruang eigen yang bersesuaian dengan \(λ=5\), dan
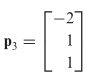
adalah sebuah basis untuk ruang eigen yang bersesuaian dengan \(λ=1\). Dengan mudah anda dapat memeriksa bahwa \(\{p_1,p_2,p_3\}\) bebas linear, sehingga

akan mendiagonalkan \(A\). Sebagai pemeriksaan, anda harus membuktikan bahwa
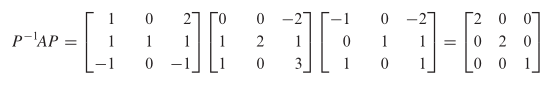
Tidak ada urutan yang diistimewakan untuk kolom-kolom P. Karena entri diagonal ke-i dari \(P^{-1} AP\) adalah nilai eigen untuk vektor kolom ke-i dari P, maka dengan mengubah urutan kolom-kolom P hanyalah mengubah urutan nilai-nilai eigen pada diagonal \(P^{-1} AP\). Jadi, seandainya kita tuliskan

di dalam contoh terakhir, maka kita akan memperoleh

Contoh 2: Matriks yang Tidak Dapat Didiagonalisasi
Persamaan karakteristik dari

adalah

Jadi, \(λ=-1\) adalah satu-satunya nilai eigen \(A\); vektor-vektor eigen yang bersesuaian dengan \(λ=-1\) adalah pemecahan-pemecahan dari \((-I-A)x=0\); yakni, dari

Pemecahan sistem ini adalah \(x_1=t, \quad x_2=t\); maka ruang eigen tersebut terdiri dari semua vektor yang berbentuk

Karena matriks \(A\) berukuran \(2 × 2\) sedangkan hanya ada satu basis vektor, maka \(A\) tidak dapat didiagonalisasi.
Contoh 3: Matriks yang Tidak Dapat Didiagonalisasi
Tunjukkan bahwa matriks berikut tidak dapat didiagonalisasi

Pembahasan:
Karakteristik polinomial dari \(A\) adalah

sehingga persamaan karakteristiknya adalah

dan nilai eigen yang berbeda dari \(A\) adalah \(λ=1\) dan \(λ=2\). Adapun basis untuk ruang eigen yang bersesuaian dengan nilai eigen yaitu
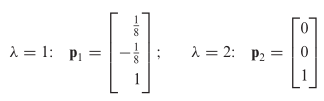
Karena matriks \(A\) berukuran \(3 × 3\) sedangkan hanya ada dua basis vektor, maka \(A\) tidak dapat didiagonalisasi.
Dalam banyak penerapan tidaklah penting menghitung matriks transisi \(P\) yang mendiagonalkan matriks \(A\) secara aktual. Sebaliknya, yang istimewa adalah mengetahui apakah \(A\) dapat didiagonalisasi. Sering, informasi ini dapat dilibatkan secara langsung dari nilai eigen tanpa melakukan kerja penghitungan vektor eigen. Untuk melihat mengapa ini sedemikian, kita membutuhkan teorema berikut.
Teorema:
Jika \(v_1,v_2,…,v_k\) adalah vektor-vektor eigen \(A\) yang bersesuaian dengan nilai-nilai eigen yang berbeda \(λ_1,λ_2,…,λ_k\), maka \({v_1,v_2,…,v_k}\) adalah himpunan bebas linear.
Sebagai konsekuensi teorema ini, kita dapatkan hasil yang berguna berikut.
Teorema:
Jika matriks \(A\) yang berukuran \(n×n\) mempunyai \(n\) nilai eigen yang berbeda, maka \(A\) dapat didiagonalisasi.
Contoh 4: Diagonalisasi Matriks
Perhatikan bahwa matriks

mempunyai 3 nilai eigen yang berbeda, \(λ=4,λ=2+\sqrt{3},λ=2-\sqrt{3}\). Dengan demikian, \(A\) dapat didiagonalisasi. Selanjutnya,

untuk suatu matriks \(P\) yang dapat dibalik. Jika diinginkan, maka matriks \(P\) dapat dicari dengan menggunakan metode yang diperlihatkan pada Contoh 1.
Perlu dicatat bahwa kebalikan dari teorema ini tidak benar; yakni, matriks \(A\) yang berukuran \(n×n\) dapat didiagonalisasi walaupun matriks tersebut tidak mempunyai \(n\) nilai eigen yang berbeda.
Contoh 5: Diagonalisasi Matriks
Misalnya, jika
\[ A = \left[ {\begin{array}{rr} 3 & 0 \\ 0 & 3\\ \end{array} } \right] \]
maka persamaan karakteristik \(A\) adalah
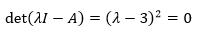
sehingga \(λ=3\) adalah satu-satunya nilai eigen \(A\). Namun \(A\) jelas dapat didiagonalisasi karena dengan \(P=I\), maka
\[ P^{-1}AP = I^{-1}AI = A = \left[ {\begin{array}{rr} 3 & 0 \\ 0 & 3\\ \end{array} } \right] \]
Diagonalisasi Matriks Segitiga
Kita tahu bahwa nilai-nilai eigen dari matriks segitiga adalah entri-entri pada diagonal utama. Oleh karena itu, matriks segitiga dengan entri-entri yang berbeda pada diagonal utama adalah dapat didiagonalisasi. Sebagai contoh, matriks

adalah matriks yang dapat didiagonalisasi dengan nilai eigen \(λ_1=-1,λ_2=3,λ_3=5,λ_4=-2\).
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
The secret of happiness you see is not found in seeking more, but in developing the capacity to enjoy less.
