www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Sistem Persamaan Linear › SPL Homogen dan Non-Homogen
SPL Homogen dan Non-Homogen
Sebuah sistem persamaan linear dikatakan homogen jika semua suku konstan sama dengan nol. Pemecahan sistem persamaan linear homogen dapat berupa pemecahan trivial dan pemecahan tak trivial.
Sebuah sistem persamaan linear dikatakan homogen jika semua suku konstan sama dengan nol, yakni sistem tersebut mempunyai bentuk

Tiap-tiap sistem persamaan linar homogen adalah sistem yang konsisten, karena \(x_1 = 0, x_2 = 0,…, x_n = 0\) selalu merupakan pemecahan. Pemecahan tersebut, dinamakan pemecahan trivial (trivial solution); jika ada pemecahan lain, maka pemecahan tersebut dinamakan pemecahan taktrivial (nontrivial solution).
Karena sistem persamaan linear homogen selalu mempunyai solusi trivial, maka hanya terdapat dua kemungkinan untuk pemecahannya, yakni:
- Sistem tersebut hanya mempunyai pemecahan trivial.
- Sistem tersebut mempunyai tak terhingga banyaknya pemecahan tak trivial.
Perhatikan kasus khusus sistem persamaan linear homogen dengan dua persamaan dan dua bilangan tak diketahui berikut:
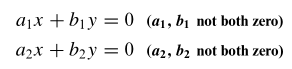
Grafik dari persamaan tersebut adalah garis yang melalui titik asal (origin), dan solusi trivial yang bersesuaian dengan titik perpotongan juga berada pada titik asal tersebut (Gambar 1).

Gambar 1. Ilustrasi SPL Homogen
Terdapat satu kasus yang sistem homogennya dipastikan mempunyai pemecahan taktrivial; yakni jika sistem tersebut melibatkan lebih banyak variabel daripada banyaknya persamaan. Untuk melihat mengapa bisa demikian, simak contoh SPL Homogen berikut dengan empat persamaan dan enam variabel.
Contoh 1:
Gunakan eliminasi Gauss-Jordan untuk menyelesaikan sistem persamaan linear homogen berikut:
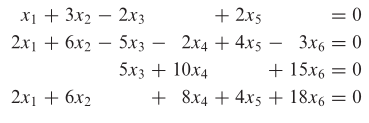
Pembahasan:
Matriks yang diperbesar (augmented matrix) untuk sistem persamaan homogen ini adalah

Dengan mereduksi matriks ini menjadi bentuk eselon baris tereduksi, maka kita dapatkan

Sistem persamaan linear yang bersesuaian adalah

Persamaan di atas dapat dituliskan kembali menjadi
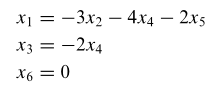
Dengan demikian, himpunan pemecahannya yaitu:

Perhatikan bahwa pemecahan trivial kita peroleh bila \(r=s=t=0\).
Teorema 1:
Sistem persamaan linear homogen dengan lebih banyak variabel daripada banyaknya persamaan selalu mempunyai tak terhingga banyaknya pemecahan.
Dari Contoh 1, kita dapat mengantisipasi bahwa sistem homogen tersebut akan memiliki banyak solusi karena memiliki empat persamaan dalam enam bilangan yang tidak diketahui.
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
It is not the load that breaks you down. It's the way you carry it.
