www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Matriks › Definisi dan Sifat-sifat Invers Matriks
Definisi dan Sifat-sifat Invers Matriks
Jika A adalah matriks kuadrat, dan jika kita dapat mencari matriks B sehingga AB = BA = I, maka A dikatakan dapat dibalik (invertible) dan B dinamakan invers (inverse) dari A.
Jika A adalah matriks kuadrat, dan jika kita dapat mencari matriks B sehingga AB = BA = I, maka A dikatakan dapat dibalik (invertible) dan B dinamakan invers (inverse) dari A.
Contoh 1: Invers Matriks
Misalkan terdapat dua matriks

Perkalian dua matriks tersebut akan menghasilkan matriks identitas, yakni
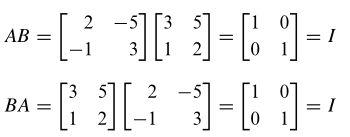
Dengan demikian, kita katakan bahwa matriks A dapat dibalik dan B adalah invers dari A.
Contoh 2: Invers Matriks
Matriks

tidak dapat dibalik. Untuk melihat mengapa demikian, misalkan matriks B berikut
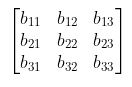
adalah sebarang matriks 3×3. Kolom ketiga dari matriks BA dapat dihitung dengan:
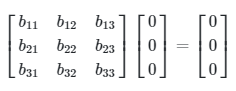
Jadi,

Selain itu, kita tahu bahwa matriks yang mempunyai baris atau kolom yang semua elemen pada baris atau kolom tersebut berisi bilangan nol akan mempunyai determinan bernilai nol dan karena itu matriks tersebut tidak dapat dibalik atau tidak mempunyai invers.
Pertanyaan yang kemudian muncul adalah apakah matriks yang dapat dibalik dapat mempunyai lebih dari satu invers. Teorema berikut ini memperlihatkan bahwa jawabannya adalah tidak – bahwa matriks yang dapat dibalik mempunyai persis satu invers.
Teorema 1:
Jika baik B maupun C adalah invers matriks A, maka B = C.
Jika A dapat dibalik, maka inversnya akan dinyatakan dengan simbol A−1. Jadi
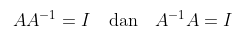
Untuk mencari invers matriks berukuran 2 x 2, kita dapat gunakan rumus berikut.

Jadi, invers dari matriks (2−5−13) adalah
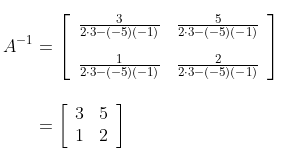
Perhatikanlah bahwa kita dapat mencari invers dari suatu matriks berukuran 2×2 dengan sangat mudah. Akan tetapi, bagaimana dengan matriks yang berukuran lebih tinggi, misalnya 3×3, 4×4 atau bahkan lebih besar dari itu? Rumus yang disediakan di atas tidak akan banyak membantu.
Oleh karena itu, pada artikel berikutnya kita akan menggunakan beberapa metode lain untuk mencari invers matriks yang dapat dibalik yang ukurannya lebih besar dari 2×2. Namun, sebelum sampai ke situ pada artikel ini kita akan terlebih dahulu memahami sifat-sifat yang ada pada invers matriks.
Sifat-sifat Invers Matriks
Teorema 2:
Jika A dan B adalah matriks-matriks yang dapat dibalik dan yang ukurannya sama, maka
(a) AB dapat dibalik
(b) (AB)−1=B−1A−1
Sebuah hasilkali matriks yang dapat dibalik selalu dapat dibalik, dan invers hasil kali tersebut adalah hasil kali invers dalam urutan yang dibalik.
Contoh 3: Sifat Invers Matriks
Tinjaulah matris-matriks

Dengan menerapkan rumus yang kita pelajari sebelumnya, kita dapatkan

dan juga

Maka, (AB)−1=B−1A−1 seperti yang ditunjukan oleh Teorema di atas.
Selanjutnya, kita akan mendefinisikan pangkat-pangkat matriks kuadrat dan membahas sifat-sifatnya terkait dengan invers matriks.
Definisi:
Jika A adalah sebuah matriks kuadrat, maka kita mendefinisikan pangkat-pangkat bilangan bulat tak negatif A menjadi

Akan tetapi, jika A dapat dibalik, maka kita mendefinisikan pangkat bilangan bulat negatif menjadi

Teorema 3:
Jika A adalah matriks kuadrat dan r serta s adalah bilangan bulat, maka

Teorema 4:
Jika A adalah sebuah matriks yang dapat dibalik, maka:
- A−1 dapat dibalik dan (A−1)−1=A
- An dapat dibalik dan (An)−1=(A−1)n untuk n=0,1,2,…
- Untuk setiap skalar k yang tak sama dengan nol, maka kA dapat dibalik dan (kA)−1=1kA−1.
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Yesterday is history; tomorrow is a mystery. Today is a gift, which is why we call it the present.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
