www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Nilai Eigen & Vektor Eigen › Basis-Basis untuk Ruang Eigen: Materi, Contoh Soal dan Pembahasan
Basis-Basis untuk Ruang Eigen: Materi, Contoh Soal dan Pembahasan
Secara definisi, vektor eigen dari matriks A yang bersesuaian dengan nilai eigen \(λ\) adalah vektor taknol dalam ruang solusi dari sistem linear yang memenuhi \((λI-A)x = 0\). Ruang solusi ini disebut ruang eigen (eigenspace) dari A yang bersesuaian dengan \(λ\).
Setelah kita mengetahui cara menemukan nilai eigen dari sebuah matriks, selanjutnya kita akan menentukan vektor eigen yang bersesuaian dengan nilai eigen tersebut. Secara definisi, vektor eigen dari matriks \(A\) yang bersesuaian dengan nilai eigen \(λ\) adalah vektor taknol yang memenuhi \[ (λI-A)x = 0 \]
Jadi, kita bisa mencari vektor eigen dari matriks \(A\) yang bersesuaian dengan \(λ\) dengan mencari vektor taknol dalam ruang solusi dari sistem linear ini. Ruang solusi ini disebut ruang eigen (eigenspace) dari \(A\) yang bersesuaian dengan \(λ\).
Contoh 1: Basis untuk Ruang Eigen
Carilah basis untuk ruang eigen dari matriks
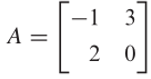
Pembahasan:
Persamaan karakteristik dari \(A\) adalah

sehingga nilai eigen dari \(A\) adalah \(λ=2\) dan \(λ=-3\). Oleh karena itu, terdapat dua ruang eigen dari \(A\), satu untuk masing-masing nilai eigen.
Secara definisi,

merupakan vektor eigen dari \(A\) yang bersesuaian dengan nilai eigen \(λ\) jika dan hanya jika \((λI-A)x=0\), yaitu,

Dalam kasus di mana \(λ=2\), persamaan ini menjadi

yang mana solusi umumnya adalah
\[ x_1 = t, \quad x_2 = t \]
Karena ini bisa ditulis dalam bentuk matriks sebagai
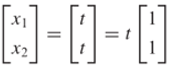
maka
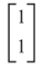
merupakan sebuah basis untuk ruang eigen yang bersesuaian dengan \(λ=2\). Dengan cara yang sama dengan di atas, maka

merupakan sebuah basis untuk ruang eigen yang bersesuaian dengan \(λ=-3\).
Contoh 2: Vektor Eigen dan Basis untuk Ruang Eigen
Carilah basis untuk ruang eigen dari matriks
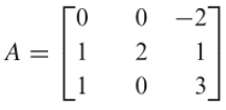
Pembahasan:
Persamaan karakteristik dari \(A\) adalah \(λ^3-5λ^2+8λ-4=0\), atau dalam bentuk faktorial, \((λ-1)(λ-2)^2=0\). Oleh karena itu, nilai eigen yang berbeda dari \(A\) adalah \(λ=1\) dan \(λ=2\), sehingga terdapat dua ruang eigen dari \(A\).
Secara definisi,

merupakan vektor eigen dari \(A\) yang bersesuai dengan \(λ\) jika dan hanya jika \(x\) merupakan solusi taktrivial dari \((λI-A)x=0\), atau dalam bentuk matriks
 |
(1) |
Dalam kasus di mana \(λ=2\), rumus (1) menjadi

Menyelesaikan sistem ini menggunakan eliminasi Gaussian akan menghasilkan

Sehingga, vektor eigen dari \(A\) yang bersesuaian dengan \(λ=2\) adalah vektor taknol dari bentuk

Karena

adalah bebas secara linear (linearly independent), maka vektor tersebut membentuk sebuah basis untuk ruang eigen yang bersesuaian dengan \(λ=2\).
Jika \(λ=1\), maka rumus (1) menjadi

Menyelesaikan sistem ini akan menghasilkan

Dengan demikian, vektor eigen yang bersesuaian dengan \(λ=1\) adalah vektor taknol dari bentuk

Sehingga

merupakan basis untuk ruang eigen yang bersesuaian dengan \(λ=1\).
Prosedur Menentukan Nilai Eigen dan Vektor Eigen
Prosedur dalam menentukan nilai eigen dan vektor eigen matriks \(A\) berukuran \(n×n\) adalah sebagai berikut:
- Tentukan polinomial karakteristik \(det(λI-A)=0\) dari matriks \(A\)
- Tentukan nilai eigen \(A\) dengan menyelesaikan persamaan karakteristik \(det(λI-A)=0\) untuk \(λ\).
- Untuk tiap nilai eigen \(λ\), tentukan ruang-null dari matriks \((λI-A)\). Vektor tak nol yang berhubungan dengan itu merupakan vektor eigen dari \(A\).
- Tentukan basis untuk ruang eigen tersebut.
Teorema berikutnya menyatakan hubungan antara nilai eigen dan keterbalikan atau invers dari suatu matriks (the invertibility of a matrix).
Teorema:
Sebuah matriks persegi \(A\) adalah dapat dibalik jika dan hanya jika \(λ=0\) bukan merupakan nilai eigen dari \(A\).
Bukti:
Asumsikan bahwa \(A\) adalah matriks berukuran \(n×n\) dan perhatikanlah bahwa \(λ=0\) adalah solusi persamaan karakteristik

jika dan hanya jika bentuk konstanta \(c_n\) adalah nol. Oleh karena itu, matriks \(A\) dapat dibalik jika dan hanya jika \(c_n≠0\).
Kita juga bisa menggunakan cara yang lain, misalnya kita tahu bahwa,

Dengan menetapkan \(λ=0\),
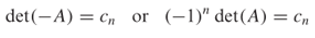
Jadi, \(det(A)=0\) jika dan hanya jika \(c_n=0\), atau matriks \(A\) dapat dibalik jika dan hanya jika \(c_n≠0\)
Contoh 3: Nilai Eigen dan Keterbalikan Suatu Matriks
Matriks \(A\) dalam Contoh 2 dapat dibalik atau mempunyai invers karena nilai eigen \(λ=1\) dan \(λ=2\), bukan bernilai nol. Anda juga bisa mengecek bahwa \(det(A)≠0\).
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
You must not lose faith in humanity. Humanity is an ocean; if a few drops of the ocean are dirty, the ocean does not become dirty.
