www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Vektor & Ruang Vektor › Proyeksi Ortogonal Vektor: Materi Contoh Soal dan Pembahasan
Proyeksi Ortogonal Vektor: Materi Contoh Soal dan Pembahasan
Dalam banyak penerapan, adalah hal yang cukup menarik untuk “menguraikan” vektor \(u\) ke dalam jumlah dua suku, yang satu sejajar dengan vektor taknol \(a\) sedangkan yang lain vektor yang tegak lurus terhadap \(a\). Jika \(u\) dan \(a\) ditempatkan sedemikian rupa, maka titik awalnya akan menempati titik \(Q\), kita akan menguraikan \(u\) sebagai berikut:

Vektor \(w_1\) sejajar dengan \(a\), vektor \(w_2\) tegak lurus dengan \(a\), dan
 |
(1) |
Karena vektor \(w_1\) sejajar dengan \(a\), maka \(w_1\) merupakan kelipatan skalar \(k\) dari \(a\):
 |
(2) |
Substitusi persamaan (2) ke persamaan (1):
 |
(3) |
Jika kita kalikan kedua sisi dengan \(a\), maka:
 |
(4) |
Sedangkan hubungan perkalian silang \(a \cdot a\) dengan panjang vektor adalah \(‖a‖^2\), dan vektor \(w_2\) tegak lurus terhadap \(a\), sehingga \(w_2 \cdot a = 0\). Maka:
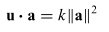 |
(5) |
Sehingga:
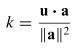 |
(6) |
Substitusi persamaan (6) ke persamaan (2), didapat:
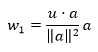 |
(7) |
Vektor w1 disebut proyeksi \(u\) pada \(a\) atau kadang-kadang komponen vektor dari \(u\) yang sejajar dengan \(a\). Dinyatakan dengan: \(proy_a \ u\)
Jika persamaan (6) disubstitusikan ke persamaan (4), didapat:
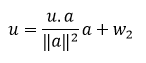 |
(8) |
 |
(9) |
atau
\[ w_2 = u - proy_a \ u \]
Vektor \(w_2\) disebut komponen vektor \(u\) yang ortogonal terhadap \(a\).
Jika \(u\) dan \(a\) adalah vektor di ruang berdimensi 2 atau ruang berdimensi 3 dan jika \(a ≠ 0\). Maka:

Panjang dari vektor komponen vektor \(u\) sepanjang \(a\) dapat diperoleh:

Contoh 1: Proyeksi Ortogonal
Anggap \(u = (2, -1, 3)\) dan \(v = (4, -1, 2)\). Cari komponen vektor dari \(u\) yang sejajar \(v\) dan komponen vektor \(u\) yang ortogonal terhadap \(v\).
Pembahasan:

Komponen vektor \(u\) yang sejajar \(v\) adalah:

Komponen vektor \(u\) yang ortogonal terhadap \(v\) adalah:
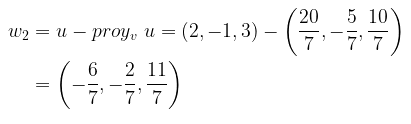
Bukti bahwa \(w_2\) ortogonal terhadap \(v\):

Contoh 2: Proyeksi Ortogonal
Diketahui \(u = (3, 2, -1)\) dan \(v = (4, 5, 2)\). Cari komponen vektor dari \(u\) yang sejajar \(v\) dan komponen vektor \(u\) yang ortogonal terhadap \(v\).
Pembahasan:
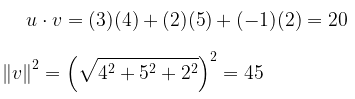
Komponen vektor \(u\) yang sejajar \(v\) adalah:

Komponen vektor \(u\) yang ortogonal terhadap \(v\) adalah:

Bukti bahwa \(w_2\) ortogonal terhadap \(v\):
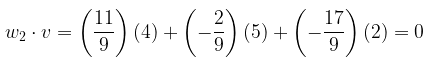
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Keep smiling, because life is a beautiful thing and there’s so much to smile about.
