www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Diagonalisasi Matriks › Diagonalisasi Ortogonal Matriks: Materi, Contoh Soal dan Pembahasan
Diagonalisasi Ortogonal Matriks: Materi, Contoh Soal dan Pembahasan
Matriks A kuadrat dikatakan dapat didiagonalisasi secara ortogonal jika terdapat matriks P yang ortogonal sehingga \( P^{-1} AP = P^T AP \) diagonal; matriks P dikatakan mendiagonalisasi A secara ortogonal.
Matriks \(A\) kuadrat dinamakan dapat didiagonalisasi secara ortogonal jika terdapat matriks \(P\) yang ortogonal sehingga \(P^{-1}AP=P^TAP\) diagonal; matriks \(P\) dikatakan mendiagonalisasi \(A\) secara ortogonal.
Perlu diingat bahwa matriks ortogonal adalah suatu matriks khusus di mana invers-nya dapat diperoleh dengan mentransposkan. Dengan kata lain, sebuah matriks persegi P dikatakan ortogonal jika transposnya sama dengan inversnya.
Kita mempunyai dua pertanyaan yang akan ditinjau:
- Matriks-matriks manakah yang dapat didiagonalisasi secara ortogonal?
- Bagaimana kita mencari matriks ortogonal untuk melaksanakan diagonalisasi?
Untuk membantu kita menjawab pertanyaan pertama kita perlu memahami definisi matriks simetris.
Definisi:
Matriks \(A\) kuadrat kita namakan simetrik jika \(A = A^T\).
Contoh 1: Matriks Simetris
Jika
\[ A = \left[ {\begin{array}{rr} 1 & 4 & 5 \\ 4 & -3 & 0 \\ 5 & 0 & 7 \\ \end{array} } \right] \]
adalah simetris, maka
\[ A^T = \left[ {\begin{array}{rr} 1 & 4 & 5 \\ 4 & -3 & 0 \\ 5 & 0 & 7 \\ \end{array} } \right] = A \]
Dengan demikian matriks \(A\) dikatakan simetris.
Teorema berikut ini merupakan alat utama untuk menentukan apakah sebuah matriks dapat didiagonalisasi secara ortogonal.
Teorema:
Jika \(A\) adalah matriks \(n×n\), maka pernyataan berikut ekivalen satu sama lain.
- \(A\) dapat didiagonalisasi secara ortogonal.
- \(A\) mempunyai himpunan ortonormal dari \(n\) vektor eigen.
- \(A\) adalah simetrik
Sifat-Sifat Matriks Simetris
Kita sekarang beralih ke masalah untuk mencari matriks \(P\) yang ortogonal untuk mendiagonalisasi matriks simetris. Kuncinya ada pada teorema berikut:
Teorema:
Jika \(A\) adalah matriks simetris, maka vektor-vektor eigen dari ruang eigen yang berbeda akan ortogonal.
Contoh 2: Diagonalisasi Ortogonal Matriks
Carilah matriks ortogonal \(P\) yang mendiagonalisasi

Pembahasan:
Persamaan karakteristik \(A\) adalah
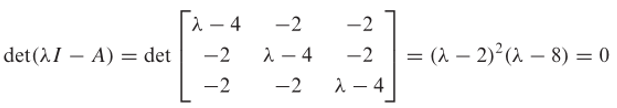
Jadi, nilai-nilai eigen \(A\) adalah \(λ=2\) dan \(λ=8\). Adapun vektor-vektor

membentuk basis untuk ruang eigen yang bersesuaian dengan \(λ=2\). Dengan menerapkan proses Gramm-Schmidt terhadap \(\{u_1,u_2\}\) akan menghasilkan vektor-vektor eigen ortonormal.

Ruang eigen yang bersesuaian dengan \(λ=8\) mempunyai
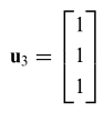
sebagai basis. Dengan menerapkan proses Gramm-Schmidt terhadap \(\{u_3\}\) maka akan menghasilkan
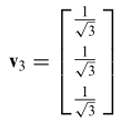
Akhirnya, dengan menggunakan \(v_1,v_2,\) dan \(v_3\) sebagai vektor-vektor kolom maka kita dapatkan
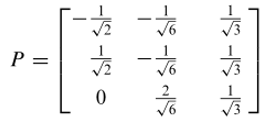
yang akan mendiagonalisasi \(A\) secara ortogonal. (Sebagai pemeriksaan, anda bisa membuktikan bahwa \(P^TAP\) adalah matriks diagonal).

Kita simpulkan bagian ini dengan menyatakan dua sifat penting dari matriks simetrik.
Teorema:
- Persamaan karakteristik matriks \(A\) simetrik hanya mempunyai akar-akar riil.
- Jika nilai eigen \(λ\) dari matriks simetrik \(A\) diulangi \(k\) kali sebagai akar persamaan karakteristik tersebut, maka ruang eigen yang bersesuaian dengan \(λ\) adalah ruang berdimensi \(k\).
Contoh 3: Diagonalisasi Ortogonal Matriks
Persamaan karakteristik matriks simetrik

adalah

sehingga nilai-nilai eigen adalah \(λ=4,λ=1\), dan \(λ=2\), di mana \(λ=4\) dan \(λ=1\) diulangi dua kali dan \(λ=2\) terjadi sekali. Jadi ruang-ruang eigen yang bersesuaian dengan \(λ=4\) dan \(λ=1\) adalah ruang berdimensi 2 dan ruang eigen yang bersesuaian dengan \(λ=2\) adalah ruang berdimensi 1.
Sumber:
Anton, Howard & Chris Rorres. 2014. Elementary linear algebra : applications version, 11th edition. John Wiley & Sons, Inc: Hoboken, New Jersey.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
It’s never too late – never too late to start over, never too late to be happy.
