Statistika Matematika I   »   Distribusi Sampling   ›  Teorema Limit Pusat

Peubah Acak

Teorema Limit Pusat

Teorema Limit Pusat (Central Limit Theorem) menyatakan bahwa bentuk distribusi sampling dari rata-rata sampel selalu cenderung mendekati distribusi normal.

Terdapat sebuah teorema penting terkait distribusi sampling yang dikenal dengan Teorema Limit Pusat (Central Limit Theorem). Teorema ini menyatakan bahwa bentuk distribusi sampling dari rata-rata sampel selalu cenderung mendekati distribusi normal. Kita nyatakan dalam teorema berikut.

Teorema Limit Pusat

Jika sampel acak berukuran \(n\) ditarik dari populasi dengan rata-rata \(μ\) dan varians \(σ^2\), maka rata-rata sampel \(\overline{X}\) akan mempunyai distribusi yang mendekati distribusi normal dengan rata-rata \(μ\) dan varians \(σ^2/n\). Jadi, distribusi fungsi

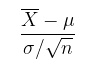
akan mendekati (mengaproksimasi) normal standar (approximately a standard normal). Aproksimasi akan semakin tepat seiring dengan meningkatnya ukuran sampel.

Untuk mendapatkan gambaran mengenai teorema limit pusat, perhatikanlah Gambar 1 berikut. Gambar 1 menunjukkan tiga populasi berbeda yang mana dari populasi tersebut diambil sampel acak berukuran n = 2, 5, 10 dan 25. Distribusi sampling dari rata-rata sampel juga ditunjukkan pada Gambar 1.

Gambar 1. Distribusi sampling dari rata-rata sampel

Perhatikan bahwa, saat sampel diambil dari populasi berdistribusi normal, distribusi sampling dari rata-rata sampel juga berdistribusi normal terlepas dari ukuran sampelnya (bahkan untuk sampel kecil). Untuk distribusi yang tidak simetris atau normal, distribusi sampling-nya adalah menceng (skewed) untuk sampel kecil, tetapi untuk n = 25, distribusi sampling-nya mendekati atau hampir simetris (normal).

Teorema Limit Pusat memberikan hasil yang sangat bermanfaat untuk inferensia statistik. Perhatikan bahwa \(\overline{X}\) adalah peubah acak dan mempunyai distribusi peluang. Untuk n besar, distribusi sampling dari \(\overline{X}\) akan mendekati distribusi normal. Lebih tepatnya, untuk n besar, kita bisa menemukan

di mana Z adalah peubah acak normal standar.

Contoh 1:

Misalkan sampel acak berukuran n = 25, 50, dan 100 diambil dari populasi yang mempunyai fungsi kepekatan peluang eksponensial dengan rata-rata 10 dan variansnya juga bernilai 10 \((σ=10)\). Temukan interval (a,b) untuk tiap n sehingga \(P(a ≤ \overline{X} ≤ b)=0.95\).

Pembahasan:

Dari Teorema Limit Pusat, kita tahu bahwa distribusi \( \overline{X} \) akan mendekati normal dengan rata-rata dan standar deviasi

yang nilainya ditunjukkan pada tabel berikut

Perhatikan bahwa \(P(a ≤ \overline{X} ≤ b)=0.95\) akan setara atau ekivalen dengan

Karena \(Z=\sqrt{n}(\overline{X}-μ)/σ\) akan mempunyai distribusi yang mendekati distribusi normal standar, maka pertidaksamaan ini bisa diaproksimasi dengan

Namun, kita tahu bahwa \(P(-1.96≤Z≤1.96)=0.95\). Dengan membandingkan kedua pernyataan ini, kita peroleh

Ini memberikan \(a=μ-1.96σ/\sqrt{n}\) dan \(b=μ+1.96σ/\sqrt{n}\). Tabel berikut memberikan interval untuk ukuran sampel yang berbeda. Perhatikan bahwa persebaran distribusi sampling menurun ketika ukuran sampel meningkat (Anda dapat mengamati Gambar 1 di atas sebagai contoh). Akibatnya, interval (a,b) menjadi lebih pendek ketika n meningkat.