
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA MATEMATIKA I
Statistika Matematika I
Peubah Acak dan Distribusi Peubah Acak
Distribusi Bersama Peubah Acak
Sifat Peubah Acak
Distribusi Fungsi Peubah Acak
Distribusi Sampling
Statistika Matematika I » Distribusi Peubah Acak › Distribusi Peubah Acak Diskrit
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Peubah Acak
Distribusi Peubah Acak Diskrit
Banyak kejadian atau peristiwa dalam kehidupan kita sehari-hari yang mengikuti distribusi peubah acak diskrit.
Jika suatu ruang sampel mengandung titik yang terhingga banyaknya atau sederetan anggota yang banyaknya sebanyak bilangan bulat, maka ruang sampel itu disebut ruang sampel diskret dan peubah acak yang didefinisikan tersebut disebut peubah acak diskrit.
Banyak kejadian atau peristiwa dalam kehidupan sehari-hari yang mengikuti salah satu dari distribusi peubah acak diskrit yang akan diberikan berikut ini.
Distribusi Uniform Diskrit
Bila peubah acak X mendapat nilai x1,x2,…,xn dengan peluang yang sama, maka distribusi seragam diskret diberikan oleh

Lambang f(x;n) dipakai sebagai pengganti f(x) untuk menunjukkan bahwa distribusi seragam tersebut bergantung pada parameter n.
Rataan dan Varians
Rataan dan variansi distribusi seragam diskret f(x;n) adalah

atau bisa juga dinyatakan dengan

Moment Generating Function
Fungsi pembangkit momen atau moment generating function (MGF) dari distribusi uniform diskrit yaitu:

Distribusi Bernoulli
Fungsi kepadatan peluang distribusi Bernouli adalah

di mana x merupakan nilai peubah acak, p merupakan parameter di mana 0≤p≤1. Peubah acak X yang berdistribusi Bernoulli dapat ditulis X∼Bernoulli(p).
Rataan dan Varians
Rataan atau nilai harapan peubah acak X yang berdistribusi bernoulli adalah p sedangkan variansnya adalah pq.
Moment Generating Function
Fungsi pembangkit momen atau fungsi MGF dari distribusi bernoulli yaitu

Distribusi Binomial
Jika suatu usaha Bernoulli menghasilkan sukses dengan peluang p dan gagal dengan peluang q=1−p, maka distribusi peluang peubah acak Binomial X, yaitu banyaknya sukses dalam n usaha bebas, ialah
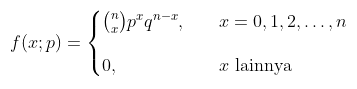
Rataan dan Varians
Nilai harapan atau rataan dari distribusi binomial yaitu np sedangkan variannya adalah npq.
Moment Generating Function
Fungsi pembangkit momen atau fungsi MGF dari distribusi binomial adalah

Distribusi Binomial Negatif
Distribusi Binomial Negatif memiliki ciri bahwa peubah acak X menyatakan banyaknya percobaan yang diperlukan untuk mendapatkan sebanyak k sukses. Bila usaha yang saling bebas, dilakukan berulang kali dan menghasilkan sukses dengan peluang p sedangkan gagal dengan peluang q=1−p, maka distribusi peluang peubah acak X, yaitu banyaknya usaha yang berakhir tepat pada sukses ke k, diberikan oleh
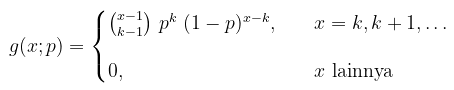
Rataan dan varians
Rataan dan varians dari distribusi binomial negatif yaitu

Moment Generating Function
Fungsi pembangkit momen atau fungsi MGF dari distribusi binomial negatif adalah
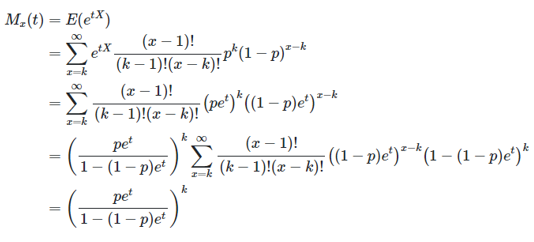
Distribusi Geometrik
Distribusi Geometrik memiliki ciri bahwa peubah acak X menyatakan banyaknya percobaan untuk mendapatkan sukses yang pertama. Bila usaha yang saling bebas dilakukan berulang kali dan menghasilkan sukses dengan peluang p, gagal dengan peluang q=1−p, maka distribusi peluang peubah acak X, yaitu banyaknya usaha sampai saat terjadi sukses yang pertama, diberikan oleh
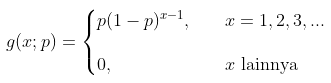
Rataan dan varians
Rataan dan varians dari distribusi geometrik adalah

Moment Generating Function
Fungsi pembangkit momen atau fungsi MGF dari distribusi geometrik adalah
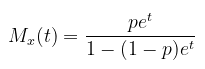
Distribusi Hipergeometrik
Distribusi peluang peubah acak hipergeometrik X, yaitu banyaknya sukses dalam sampel acak ukuran n yang diambil dari N benda yang mengandung k bernama sukses dan N−k bernama gagal, ialah

Rataan dan Varians
Rataan dan Varians distribusi hipergeometrik h(x;N,n,k) adalah

Distribusi Poisson
Distribusi peluang peubah acak Poisson X, yang menyatakan banyaknya sukses yang terjadi dalam suatu selang waktu atau daerah tertentu diberikan oleh

λ menyatakan rata-rata banyaknya sukses yang terjadi per satuan waktu atau daerah tersebut dan e=2,71823…
Teorema:
Rataan dan variansi distribusi Poisson p(x;λ) keduanya sama dengan λ.
Moment Generating Function
Fungsi pembangkit momen atau moment generating function (MGF) dari distribusi Poisson yaitu:

Artikel Terkait
Bila kamu tak tahan lelahnya belajar, maka kamu akan menanggung perihnya kebodohan.
Anonim