Kovarian (Covariance) Dua Peubah Acak

Statistika Matematika I » Sifat Peubah Acak › Kovarian (Covariance) Dua Peubah Acak - Rumus dan Contoh Soal

Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Peubah Acak

Kovarian (Covariance) Dua Peubah Acak - Rumus dan Contoh Soal

Kovarian adalah ukuran dalam statistik untuk melihat bagaimana perubahan dalam satu variabel dikaitkan dengan perubahan dalam variabel kedua.

Kovarian adalah ukuran dalam statistik untuk melihat bagaimana perubahan dalam satu variabel dikaitkan dengan perubahan dalam variabel kedua. Secara khusus, kovarians mengukur sejauh mana dua variabel terkait secara linear.

Definisi:

Kovarians dari pasangan random variables \(X\) dan \(Y\) didefinisikan oleh

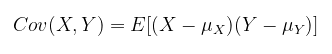
Notasi umum yang lain untuk kovarians adalah \(σ_{XY}\).

Beberapa sifat yang bermanfaat dalam menangani kovarians diberikan dalam teorema-teorema berikut:

Teorema:

Jika \(X\) dan \(Y\) adalah random variables dan \(a\) dan \(b\) adalah konstan, maka

Bukti:

Teorema:

Jika \(X\) dan \(Y\) adalah random variables dan \(a\) dan \(b\) adalah konstan, maka

Bukti:

Teorema:

Jika \(X\) dan \(Y\) adalah random variables dan \(a\) dan \(b\) adalah konstan, maka

Bukti:

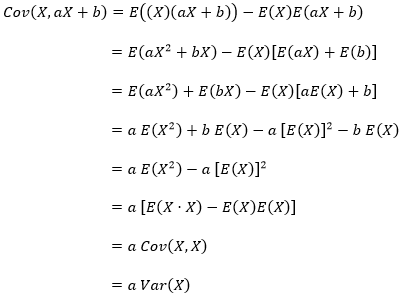
Teorema:

Jika \(X\) dan \(Y\) adalah random variables dan \(a\) dan \(b\) adalah konstan, maka

Bukti:

Teorema:

Jika \(X\) dan \(Y\) adalah random variables, maka

dan \(Cov(X,Y)=0\) ketika \(X\) dan \(Y\) adalah independen.

Teorema:

Jika \(X\) dan \(Y\) adalah random variables dengan joint pdf \(f(x,y)\), maka

dan ketika \(X\) dan \(Y\) adalah independen, maka

Bukti:

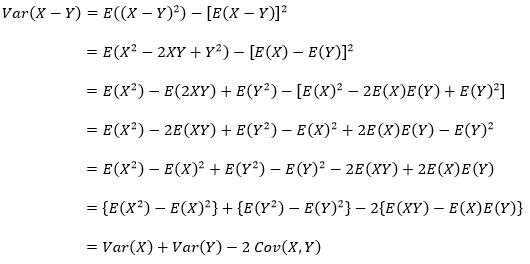
Teorema yang ada sebelumnya bisa diperluas untuk \(k\)-random variables \(X_1,…,X_k\) dan \(a_1,…,a_k\) bilangan konstan, sehingga

dan jika \(X_1,…,X_k\) adalah independen, maka

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

STATISTIKA MATEMATIKA I

Statistika Matematika I » Sifat Peubah Acak › Kovarian (Covariance) Dua Peubah Acak - Rumus dan Contoh Soal

Peubah Acak