Korelasi (Correlation) Dua Peubah Acak

Statistika Matematika I » Sifat Peubah Acak › Korelasi (Correlation) Dua Peubah Acak - Rumus dan Contoh Soal

Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Peubah Acak

Korelasi (Correlation) Dua Peubah Acak - Rumus dan Contoh Soal

Korelasi atau biasa juga disebut koefisien korelasi, adalah nilai yang menunjukkan kekuatan dan arah hubungan linier antara dua peubah acak.

Korelasi atau biasa juga disebut koefisien korelasi, adalah nilai yang menunjukkan kekuatan dan arah hubungan linier antara dua peubah acak. Korelasi positif terjadi apabila kenaikan nilai pada suatu variabel juga diikuti oleh peningkatan pada variabel lainnya.

Definisi:

Jika \(X\) dan \(Y\) adalah random variables dengan varians \(σ_X^2\) dan \(σ_Y^2\) dan kovarians \(σ_{XY}\), maka koefisien korelasi dari \(X\) dan \(Y\) adalah

Nilai \(ρ\) berada dalam rentang -1 dan 1 \((-1≤ρ≤1)\) dan jika \(X\) dan \(Y\) adalah independen, maka \(ρ=0\) (\(X\) dan \(Y\) tidak berkorelasi), tetapi \(ρ=0\) tidak berarti independen.

Contoh 1:

Perhatikan random variables \(X\) dan \(Y\) dengan joint pdf yang berbentuk \(f(x,y)= \frac{1}{20}\) jika \((x,y) ∈ C\), dan zero otherwise, di mana:

yang mana ditunjukkan pada Gambar berikut:

Gambar 1. Wilayah yang bersesuaian untuk \(0 < x < 10\) dan \(x-1 < y < x+1\)

Meskipun \(Y\) bukan fungsi dari \(X\), distribusi bersama dari \(X\) dan \(Y\) adalah “mengelompok” di sekitar garis \(y=x\), sehingga diharapkan nilai \(ρ\) akan mendekati 1.

Varians dari X dan Y adalah

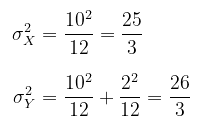
dan kovarians adalah

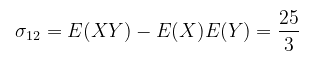
Dengan demikian, koefisien korelasi nya adalah

di mana seperti yang diharapkan yaitu mendekati 1.

Contoh 2:

Apabil \(ρ_{xy}=0\), artinya tidak ada hubungan linear antara \(X\) dan \(Y\). Namun demikian, secara matematik bukan berarti tidak ada hubungan fungsional antara \(X\) dan \(Y\). Buktikan pernyataan tersebut berdasarkan permasalahan berikut:

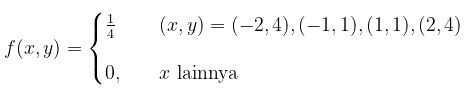
Tunjukkan bahwa \(ρ_{xy}=0\)
Gambarlah grafik kartesian (grafik 2 dimensi) yang menunjukkan hubungan fungsional matematik antara \(X\) dan \(Y\). Hubungan fungsional matematik apakah yang terjadi antara \(X\) dan \(Y\)?

Pembahasan:

Bagian (a)

Bagian (b)

Meskipun telah dibuktikan bahwa \(ρ_{xy}=0\), yang artinya tidak ada hubungan linear antara \(X\) dan \(Y\), namun bukan berarti tidak ada hubungan fungsional antara \(X\) dan \(Y\). Hal ini terbukti pada Gambar berikut di mana \(X\) dan \(Y\) memiliki hubungan kuadratik.

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

STATISTIKA MATEMATIKA I

Statistika Matematika I » Sifat Peubah Acak › Korelasi (Correlation) Dua Peubah Acak - Rumus dan Contoh Soal

Peubah Acak