
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA MATEMATIKA I
Statistika Matematika I
Peubah Acak dan Distribusi Peubah Acak
Distribusi Bersama Peubah Acak
Sifat Peubah Acak
Distribusi Fungsi Peubah Acak
Distribusi Sampling
Statistika Matematika I » Distribusi Sampling › Distribusi Sampling - Distribusi Chi-square
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Peubah Acak
Distribusi Sampling - Distribusi Chi-square
Distribusi Chi-Square banyak digunakan dalam bidang statistika. Beberapa manfaat dari distribusi Chi-square seperti menguji signifikansi antara frekuensi yang diamati dengan frekuensi teoritis dan menguji kebebasan antar faktor pada tabel kontingensi.
Gambar 1 di bawah adalah contoh kurva distribusi chi-square.

Gambar 1. Kurva chi-square
Ada pun fungsi kepadatan peluang dari distribusi chi-square dinyatakan dengan

Teorema:
Jika variabel \(Y\) berdistribusi gamma dengan parameter \(θ=2\) dan \(K=v/2\) yakni \(Y \sim GAM(2,v/2)\), maka variabel \(Y\) juga mengikuti distribusi chi-square dengan derajat bebas \(v\) yaitu \( Y \sim χ^2(v) \).
Bukti:
MGF untuk distribusi gamma dengan parameter \(θ=2\) dan \(K=v/2\) adalah

Sedangkan MGF untuk distribusi chi-square dengan derajat v adalah

Jadi, karena MGF kedua distribusi sama maka terbukti bahwa distribusi gamma dengan parameter \(θ=2\) dan \(K=v/2\) sama dengan distribusi chi-square dengan derajat bebas \(v\).
Teorema:
Jika \(X \sim GAM(θ,K)\), maka

Teorema:
Jika \(Y_i \sim χ^2 (v_i); \ i=1,…,n\) adalah variabel chi-square yang independen, maka

Teorema:
Jika \(Z \sim N(0,1)\), maka \(Z^2 \sim χ_{(1)}^2\).
Bukti:

Misalkan \( u^2 = z^2 (1-2t) \), maka \( u = z \sqrt{1-2t} \) dan \( du = \sqrt{1-2t} \ dz \). Dengan demikian, kita peroleh
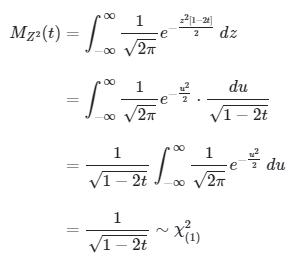
Kita tahu bahwa MGF dari chi-square dengan derajat bebas \(v\) \((χ_{(v)}^2)\) yaitu \(\frac{1}{(1-2t)^{v/2}} \) . Sehingga saat derajat bebasnya \(v = 1\) \((χ_{(1)}^2)\), maka MGF nya menjadi \(\frac{1}{\sqrt{1-2t}} \), seperti hasil yang telah kita peroleh di atas.
Teorema:
Jika \(X_1,…,X_n\) adalah sampel acak dari \(N(μ,σ^2)\), maka

Bukti:
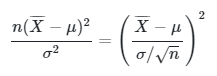
Misalkan \( Z = \frac{\overline{X}-μ}{σ/\sqrt{n}} \). Telah kita buktikan bahwa \(Z \sim N(0,1)\) sehingga
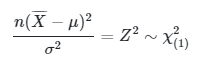
Jadi, \( \frac{n(\overline{X}-μ)^2}{σ^2} \) berdistribusi chi-square dengan derajat bebas \(v = 1. \ \ (χ_{(1)}^2)\)
Teorema:
Jika \(X_1,…,X_n\) adalah sampel acak dari \(N(μ,σ^2)\), maka

Bukti:
Misalkan \( Z = \frac{(X_i-μ)}{σ} \). Telah kita buktikan bahwa \(Z \sim N(0,1)\) dan \(Z^2 \sim χ_{(1)}^2\) dengan MGF \( \frac{1}{(1-2t)^{1/2}} \) .
Misalkan lagi \(Y=\sum_\limits{i=1}^n \frac{(X_i-μ)^2}{σ^2} \), sehingga \(Y=\sum_\limits{i=1}^n Z_i^2\) dan karena itu,

Teorema:
Jika \(X_1,…,X_n\) adalah sampel acak dari \(N(μ,σ^2)\), maka

Bukti:

Catatan:
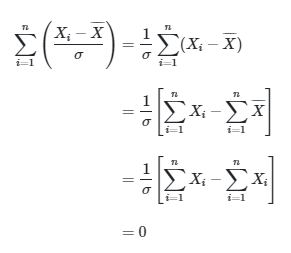
Artikel Terkait
You know you're in love when you can't fall asleep because reality is finally better than your dreams.
Dr. Seuss