
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA MATEMATIKA I
Statistika Matematika I
Peubah Acak dan Distribusi Peubah Acak
Distribusi Bersama Peubah Acak
Sifat Peubah Acak
Distribusi Fungsi Peubah Acak
Distribusi Sampling
Statistika Matematika I » Distribusi Sampling › Distribusi Sampling - Distribusi-t
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Peubah Acak
Distribusi Sampling - Distribusi-t
Distribusi student-t banyak diterapkan pada statistik inferensia ketika nilai varians dari suatu populasi tidak diketahui.
Distribusi student-t banyak diterapkan pada statistik inferensia ketika nilai varians dari suatu populasi tidak diketahui.
Meskipun mirip, distribusi dari peubah acak yang berdistribusi student-t dan normal yakni \(T\) dan \(Z\) adalah berbeda karena varians \(T\) bergantung pada ukuran sampel \(n\) dan varians ini selalu lebih besar dari 1. Hanya ketika ukuran sampel \(n→∞\), kedua distribusi menjadi sama.
Gambar 1 berikut memperlihatkan hubungan antara distribusi normal baku (distribusi student-t dengan derajat bebas \(v=∞\)) dan distribusi \(t\) untuk derajat bebas 2 dan 5.
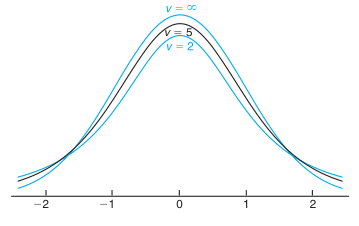
Gambar 1. Kurva distribusi-t untuk \( v=2, 5, \) dan \(∞\)
Kita bisa mendefinisikan peubah acak \(T\) yang mengikuti distribusi student-t sebagai rasio dari peubah acak normal baku \(Z\) terhadap peubah acak chi-square \(V\) dengan derajat bebas \(v\).
Definisi:
Jika \(X_1 \sim N(0,1)\) dan \(X_2 \sim χ^2 (n)\), dan jika \(X_1\) dan \(X_2\) adalah independen, maka variabel

akan mengikuti distribusi student-t dengan derajat bebas \(n\), dinotasikan dengan \(T \sim t(n)\). Pdf dari distribusi ini adalah
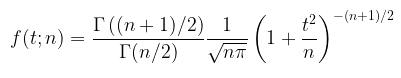
Bukti:
Pembuktian yang akan diberikan berikut cukup rumit dan melibatkan teknik transformasi yang telah kita pelajari. Jika Anda kurang paham, bertanyalah kepada yang lain. Tidak perlu terlalu memaksakan diri.

Misalkan,

Sehingga
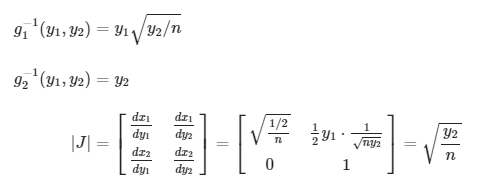

Mencari distribusi dari \( f_{y_1} (y_1) \), yakni

Gunakan rumus:

di mana:

Dengan demikian, kita peroleh
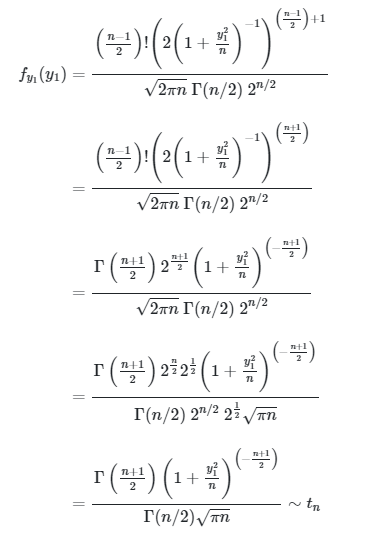
Salah satu teorema penting berkaitan dengan distribusi student-t diberikan berikut ini.
Teorema:
Jika \(X_1,X_2,…,X_n\) adalah sampel acak dari \(N(μ,σ^2)\), maka

Bukti:

Misalkan \( Z = \frac{\overline{X}-μ}{σ/\sqrt{n}} \). Telah kita buktikan bahwa \(Z \sim N(0,1)\) dan \( \frac{(n-1) S^2}{σ^2} \sim χ_{(n-1)}^2 \). Sehingga
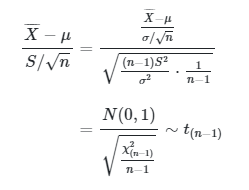
Artikel Terkait
Bila kamu tak tahan lelahnya belajar, maka kamu akan menanggung perihnya kebodohan.
Anonim