
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA MATEMATIKA I
Statistika Matematika I
Peubah Acak dan Distribusi Peubah Acak
Distribusi Bersama Peubah Acak
Sifat Peubah Acak
Distribusi Fungsi Peubah Acak
Distribusi Sampling
Statistika Matematika I » Distribusi Fungsi Peubah Acak › Teknik Transformasi Bukan Satu-Satu
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Peubah Acak
Teknik Transformasi Bukan Satu-Satu
Teknik transformasi untuk mencari distribusi suatu peubah acak baru dapat dibagi jadi dua yakni transformasi satu-satu dan transformasi yang bukan satu-satu.
Misalkan \(X\) adalah peubah acak dengan pdf \(f_X (x)\). Jika \(Y=g(X)\) merupakan fungsi yang bukan satu-satu, maka tidak ada solusi unik untuk persamaan \(Y = g(X)\). Walaupun demikian, terdapat kemungkinan untuk mempartisi atau memecah \(A=\{x | f_X (x)>0\}\) ke dalam beberapa subset yang saling lepas (disjoint) yakni \(A_1,A_2,…\) sedemikian rupa sehingga \(Y=g(X)\) adalah fungsi satu-satu untuk masing-masing \(A_j\).
Dengan demikian, untuk masing-masing \(Y\) dalam range \(g(X)\), persamaan \(Y=g(X)\) memiliki solusi yang unik yaitu \(x_j=g_j^{-1} (y)\) untuk tiap himpunan \(A_j\). Dalam kasus diskrit, maka transformasi yang tidak satu-satu diberikan oleh

dan untuk kasus kontinu, maka

Contoh 1: Kasus Diskrit
Andaikan \(X\) adalah peubah acak diskrit dengan pdf
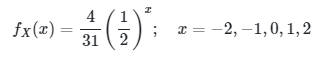
Jika \(Y = |X|\), maka tentukanlah pdf dari \(Y\).
Pembahasan:
Karena \(Y = |X|\) dan \(A = \{ x = -2, -1, 0, 1, 2 \}\), maka jelas \(B = \{0, 1, 2\}\). Sehingga
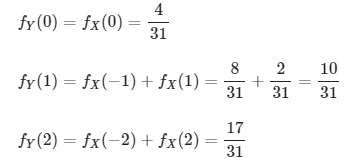
Cara lain untuk menyatakan ini adalah
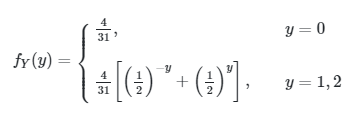
Contoh 2: Kasus Kontinu
Misalkan \(X\) adalah peubah acak kontinu yang mengikuti distribusi uniform, yakni \(X \sim UNIF(-1,1)\) dengan pdf

Jika \(Y=X^2\), tentukanlah \(f_Y (y)\).
Pembahasan:
Perhatikan bahwa \(Y=X^2\) di mana \(A = (-1,1)\) merupakan fungsi yang tidak satu-satu sehingga tidak ada solusi unik untuk \(Y=X^2\). Namun, kita masih dapat memperoleh solusi unik dengan cara mempartisi \(A = (-1,1)\) menjadi \(A_1=(-1,0)\) dan \(A_2=(0,1)\). Sehingga, solusi uniknya adalah

Dengan demikian, pdf dari \(Y\) adalah

Hal yang perlu diperhatikan adalah jika batasan (limits) pada fungsi \(g(X)\) tidak sama terhadap tiap himpunan partisi \(A_j\). Kita nyatakan hal ini dalam contoh berikut.
Contoh 3: Kasus Kontinu
Misalkan \(X\) adalah peubah acak kontinu dengan pdf
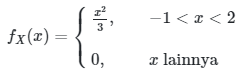
Jika \(Y=X^2\), tentukanlah pdf dari \(Y\).
Pembahasan:
Perhatikan bahwa untuk \(x < 0\) kita peroleh invers transformasi yakni \(x_1=g_1^{-1} (y)=-\sqrt{y}\) dan \(x_2=g_1^{-1} (y)=\sqrt{y}\) untuk \(x > 0\). Namun, untuk \(0 < y < 1\) terdapat dua titik dengan pdf tak nol, yakni \(x_1=-\sqrt{y}\) dan \(x_2=\sqrt{y}\); sedangkan untuk \(1 < y < 4\) terdapat hanya satu titik dengan pdf tak nol, yakni \(x_2=\sqrt{y}\). Dengan demikian pdf dari \(Y\) adalah
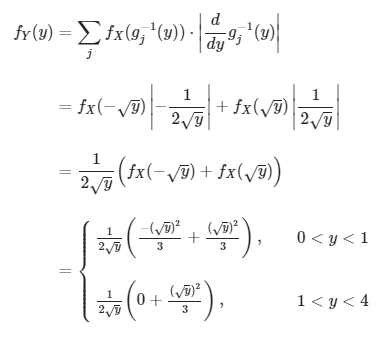
Artikel Terkait
Di dalam membagi waktu kerja sebaiknya harus ada waktu yang terluang meskipun sedikit untuk sekedar beristirahat melepas lelah, karena hati atau jiwa juga merasa lelah dan bosan seperti halnya tubuh atau raga.
Dr. Yusuf Al-Qaradhawi