Statistika Matematika I   »   Distribusi Bersama Peubah Acak   ›  Distribusi Marginal (Marginal Distribution) - Rumus dan Contoh Soal

Peubah Acak

Distribusi Marginal (Marginal Distribution) - Rumus dan Contoh Soal

Distribusi salah satu peubah acak yang diturunkan dari suatu distribusi gabungan (joint distribution) disebut distribusi marginal.

Dalam statistik tingkat lanjut, pembahasan tidak lagi hanya terkait satu variabel atau peubah acak melainkan melibatkan beberapa peubah acak. Distribusi dari beberapa peubah acak disebut distribusi gabungan (joint distribution).

Namun, adakalanya kita tertarik hanya pada salah satu dari beberapa variabel acak tersebut. Distribusi salah satu peubah acak yang diturunkan dari suatu distribusi gabungan (joint distribution) disebut distribusi marginal.

Sebagai contoh, misalkan diketahui distribusi dari data bivariat atau distribusi dari dua variabel acak, katakanlah \(X\) dan \(Y\), adalah \(f(x,y)\). Dengan demikian, distribusi peubah acak \(X\) yang dinyatakan sebagai \(f(x)\) atau distribusi peubah acak \(Y\) yakni \(f(y)\) disebut distribusi marginal.

Untuk lebih jelasnya kita definisikan distribusi marginal sebagai berikut:

Contoh 1: Kasus Diskrit

Diketahui fungsi distribusi peluang bersama (joint pdf) dari peubah acak \(X\) dan \(Y\) adalah:

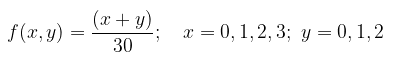
Carilah pdf marginal dari \(X\) dan \(Y\).

Pembahasan:

Karena \(X\) dan \(Y\) adalah peubah-peubah acak diskrit, maka kita gunakan rumus mencari distribusi marginal untuk kasus diskrit. Pdf marginal dari \(X\), yaitu

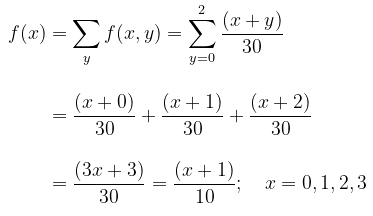
dan pdf marginal dari \( Y \) adalah

Contoh 2: Kasus Kontinu

Jika diketahui pdf bersama (joint pdf) dari \(X\) dan \(Y\) adalah

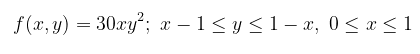
Carilah pdf marginal dari \(X\) dan \(Y\).

Pembahasan:

Karena \(X\) dan \(Y\) adalah peubah-peubah acak kontinu, maka kita gunakan rumus mencari distribusi marginal untuk kasus kontinu. Pdf marginal dari \(X\), yaitu

dan pdf marginal dari \( Y \) adalah