Statistika Matematika I   »   Sifat Peubah Acak   ›  MGF Bersama (Joint MGF) - Rumus dan Contoh Soal

Joint MGF

MGF Bersama (Joint MGF) - Rumus dan Contoh Soal

Pada artikel ini kita akan membahas perluasan dari fungsi pembangkit momen (moment generating function/MGF) untuk kasus banyak peubah (multivariate).

Dalam kasus univariat, fungsi pembangkit momen (moment generating function, MGF) dari peubah acak \(X\), yang dinotasikan dengan \(M_X(t)\), diberikan oleh:

untuk semua nilai \(t\) di mana nilai harapannya ada.

Fungsi pembangkit momen bisa didefinisikan menurut peubah acak diskrit dan kontinu, yakni

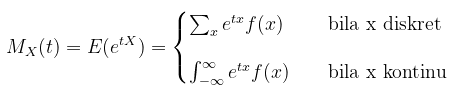
Sekarang, kita akan membahas perluasan dari fungsi pembangkit momen untuk kasus banyak peubah (multivariate). Untuk fungsi pembangkit momen univariat, baca artikel ini: Fungsi Pembangkit Momen Univariat

Fungsi Pembangkit Momen Bersama (Joint MGF)

Andaikan \(X\) dan \(Y\) adalah peubah acak yang mempunyai fungsi kepadatan peluang bersama (joint pdf) \(f(x,y)\). Maka kita bisa definisikan fungsi pembangkit momen bersama (joint moment generating function), \(M(t_1,t_2)\), dari \(X\) dan \(Y\) sebagai berikut:

Jika \(X\) dan \(Y\) adalah saling bebas (independent), maka fungsi pembangkit momen bersama (joint mgf) menjadi

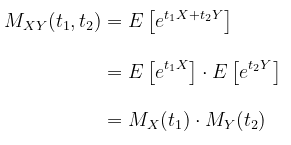
Dengan demikian, jika fungsi pembangkit momen bersama dari \(X\) dan \(Y\) adalah dalam bentuk \(M_X (t_1 )⋅M_Y (t_2)\), maka \(X\) dan \(Y\) dikatakan saling bebas (independent) dan masing-masing mempunyai mgf \(M_X (t_1)\) dan \(M_Y (t_2)\).

Definisi fungsi pembangkit momen bersama di atas adalah untuk kasus khusus dua peubah, yakni \(X\) dan \(Y\). Tentu saja, kita bisa memperluas definisi joint mgf ini untuk lebih dari dua peubah \((X_1, X_2,…,X_n)\). Kita nyatakan dalam definisi berikut:

Definisi:

Andaikan \((X_1, X_2,…,X_n)\) adalah peubah-peubah acak. Fungsi pembangkit momen bersama (joint mgf) didefinisikan sebagai berikut:

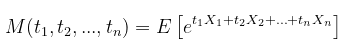
Fungsi Pembangkit Momen Marginal (Marginal MGF)

Kita bisa mencari MGF dari distribusi marginal suatu peubah acak berdasarkan MGF bersama (joint mgf) dengan menetapkan \(t = 0\) untuk \(t\) yang tidak berkaitan dengan peubah acak yang kita inginkan. Kita nyatakan definisi formalnya berikut ini.

Definisi:

Andaikan \(M_{XY} (t_1,t_2)\) adalah MGF dari \(X\) dan \(Y\), maka MGF dari distribusi marginal \(X\) dan \(Y\) masing-masing adalah

Hal yang sama berlaku untuk menurunkan MGF marginal dari MGF bersama yang terdiri lebih dari dua peubah acak.