Statistika Matematika I   »   Distribusi Fungsi Peubah Acak   ›  Teknik MGF untuk Mencari Distribusi Peubah Acak Baru

Peubah Acak

Teknik MGF untuk Mencari Distribusi Peubah Acak Baru

Sesuai dengan namanya, teknik MGF menggunakan fungsi pembangkit momen (moment generating function/MGF) untuk mencari distribusi suatu peubah acak baru.

Dua teknik untuk menemukan distribusi dari suatu peubah acak telah kita bahas pada artikel sebelumnya, yakni teknik cdf dan teknik transformasi. Sekarang, kita akan kaji teknik terakhir yaitu yang dikenal dengan teknik mgf.

Sesuai dengan namanya, teknik ini menggunakan fungsi pembangkit momen (moment generating function) untuk mencari distribusi suatu peubah acak.

Teorema:

Jika \(X\) adalah peubah acak dengan fungsi pembangkit momennya (MGF) adalah \(M_X (t)\) dan \(Y\) merupakan fungsi dari \(X\) yakni \(Y=u(x)\), maka fungsi pembangkit momen (MGF) dari peubah acak Y dapat dinyatakan dengan:

Teorema:

Jika \(X_1,X_2,…,X_n\) adalah peubah acak independen dengan fungsi pembangkit momennya (MGF) adalah \(M_{X_i}(t)\), maka fungsi pembangkit momen (MGF) dari \(Y=\sum_\limits{i=1}^n X_i\) dapat ditentukan sebagai berikut:

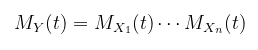
Bukti:

Karena

maka,

Teorema:

Jika \(X_1,X_2,…,X_n\) adalah sampel yang berasal dari populasi dengan fungsi kepekatan peluang (probability density function, pdf) dan fungsi pembangkit momen (moment generating function, MGF) yang sama yakni \(f(x)\) dan \(M_X (t)\), maka MGF dari \(Y=\sum_\limits{i=1}^n X_i\), yaitu:

Bukti:

\begin{aligned} M_{X+a} (t) &= E \left[ e^{t(X+a)} \right] \\[8pt] &= e^{at} \ E(e^{tX} ) \\[8pt] &= e^{at} \ M_X(t) \end{aligned}

Bukti:

\begin{aligned} M_{aX} (t) &= E \left[ e^{t(aX)} \right] \\[8pt] &= E(e^{(at)X} ) \\[8pt] &= M_X(at) \end{aligned}

Dari penjelasan di atas, kurang lengkap rasanya jika tidak disertai dengan contoh soal yang akan memperdalam pemahaman kita mengenai fungsi pembangkit momen ini. Oleh karena itu, kita akan memberikan contoh penerapan dari fungsi pembangkit momen ini.

Contoh Soal dan Pembahasan

Contoh 1:

Misal \(X_1,…,X_k\) adalah peubah acak independen yang berdistribusi binomial dengan parameter \(n_i\) dan \(p\), yakni \(X_i \sim BIN(n_i,p)\) dengan, \(M_X (t)=(pe^t+q)^n\) dan jika \(Y=∑_\limits{i=1}^k X_i\), maka

Jadi, \(Y \sim BIN(n_1+⋯+n_k,p)\).

Contoh 2:

Misalkan \(X_1,X_2,…,X_n\) adalah peubah acak bebas yang berdistribusi Poisson, yaitu \(X_i \sim Poi(μ_i)\), dan misalkan \(Y=X_1+⋯+X_n\). MGF dari \(X_i\) adalah \(M_{X_i} (t)= \text{exp⁡} \left[μ_i (e^t-1)\right]\), dan akibatnya MGF dari \(Y\) adalah

yang menunjukkan bahwa \(Y \sim POI(μ_1+⋯+μ_n)\).

Contoh 3:

Misalkan \(X_1,X_2,…,X_n\) adalah peubah acak bebas yang berdistribusi Gamma dengan masing-masing parameter \(K_1,K_2,…,K_n\) dan parameter yang sama yaitu \(θ\) \((X_i \sim GAM(θ,K_i))\) untuk \(i = 1, …,n\). MGF dari \(X_i\) adalah

Jika \(Y=∑_\limits{i=1}^n X_i\), maka MGF dari \(Y\) adalah

Dengan demikian, \(Y \sim GAM(θ,K_1+⋯+K_n)\).

Contoh 4:

Misalkan \(X_1,X_2,…,X_n\) adalah peubah acak bebas yang berdistribusi normal, \(X_i \sim N(μ_i,σ_i^2)\), dan misalkan \(Y=∑_\limits{i=1}^n X_i\). MGF dari \(X_i\) adalah

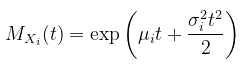
Dan karena itu MGF dari \(Y\) adalah

Dengan demikian,